An Intro to Wavelets for Computer Musicians
I wasn’t able to get this post fully complete in time for my self-imposed monthly deadline. I have decided to put it up in an incomplete state and clean it up in early September. I hope it is informative even in its current condition, which gets increasingly sketchy towards the end. Open during construction.
Among DSP types, those unfamiliar with wavelets often view them as a mysterious dark art, vaguely rumored to be “superior” to FFT in some way but for reasons not well understood. Computer musicians with a penchant for unusual and bizarre DSP (for instance, people who read niche blogs devoted to the topic) tend to get particularly excited about wavelets purely for their novelty. Is the phase vocoder too passé for you? Are you on some kind of Baudelairean hedonic treadmill where even the most eldritch Composers Desktop Project commands bore you?
Well, here it is: my introduction to wavelets, specifically written for those with a background in audio signal processing. I’ve been writing this post on and off for most of 2023, and while I am in no way a wavelet expert, I finally feel ready to explain them. I’ve found that a lot of wavelet resources are far too detailed, containing information mainly useful to people wishing to invent new wavelets rather than people who just want to implement and use them. After you peel back those layers, wavelets are surprisingly not so scary! Maybe not easy, but I do think it’s possible to explain wavelets in an accessible and pragmatic way. The goal here is not to turn you into a wavelet guru, but to impart basic working knowledge (with some theory to act as a springboard to more comprehensive resources).
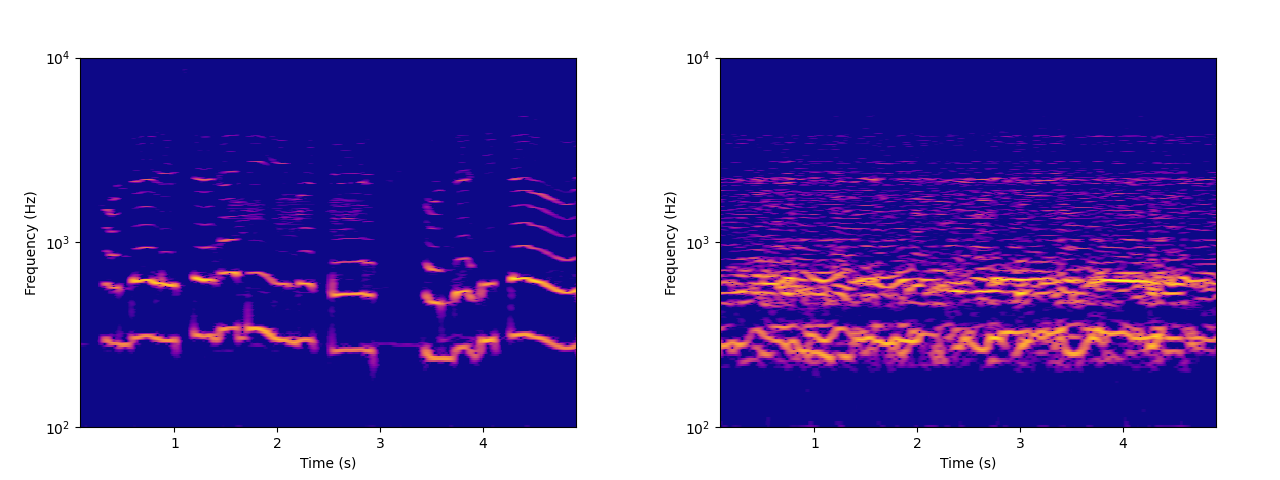
Before we go further, I have to emphasize an important fact: while wavelets have found many practical uses in image processing and especially biomedical signal processing, wavelets are not that common in audio. I’m not aware of any widely adopted and publicly documented audio compression codec that makes use of wavelets. For both audio analysis alone and analysis-resynthesis, the short-time Fourier transform and the phase vocoder are the gold standard. The tradeoffs between time and frequency resolution are generally addressable with multiresolution variants of the STFT.
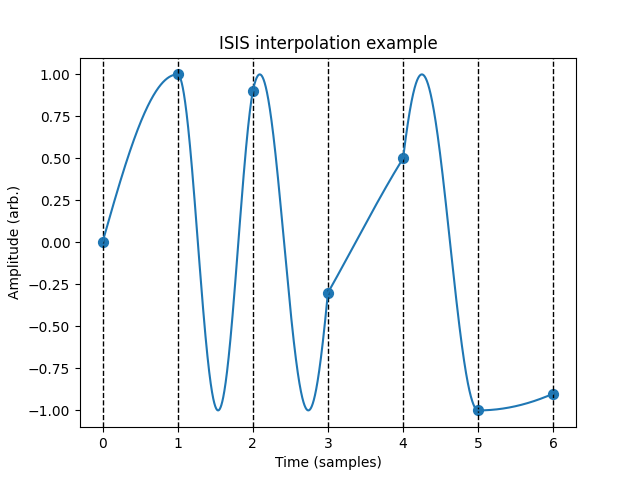
There is no one “wavelet transform” but a huge family of methods. New ones are developed all the time. To limit the scope of this post, I will introduce the two “classical” wavelet transforms: the Continuous Wavelet Transform (CWT) and Multiresolution Analysis (MRA). I’ll also go over popular choices of individual wavelets and summarize their properties. There are other wavelet transforms, some of more musically fertile than CWT or MRA, but you can’t skip the fundamentals before moving on to those. My hope is that demystifying wavelet basics will empower more DSP-savvy artists to learn about these curious creatures.