Matrix Modular Synthesis
Today’s blog post is about a feedback-based approach to experimental sound synthesis that arises from the union of two unrelated inspirations.
Inspiration 1: Buchla Music Easel
The Buchla Music Easel is a modular synthesizer I’ve always admired for its visual appearance, almost more so than its sound. I mean, look at it! Candy-colored sliders, knobs, and banana jacks! It has many modules that are well explored in this video by Under the Big Tree, and its standout features in my view are two oscillators (one a “complex oscillator” with a wavefolder integrated), two of the famous vactrol-based lowpass gates, and a five-step sequencer. The video I linked says that “the whole is greater than the sum of the parts” with the Easel – I’ll take his word for it given the price tag.
The Music Easel is built with live performance in mind, which encompasses live knob twiddling, live patching, and playing the capacitive touch keyboard. Artists such as Kaitlyn Aurelia Smith have used this synth to create ambient tonal music, which appears tricky due to the delicate nature of pitch on the instrument. Others have created more out-there and noisy sounds on the Easel, which offers choices between built-in routing and flexible patching between modules and enables a variety of feedback configurations for your bleep-bloop-fizz-fuzz needs.
Inspiration 2: CFI Model
While idly browsing the proceedings of a conference, I found a paper called “A Model for Collective Free Improvisation” by Canonne and Garnier. Written in 2011, it presents a mathematical model of a genre of experimental music deriving from free jazz. In this model (which I will call the “CFI Model”), a group of musicians listen to each other and react, with each player’s output modeled by a signal that roughly indicates the complexity of their improvisation over time. At the end of this post I’ll dig into a technical review of their research, complete with math formulas, but for now the important thing to know is that the listening process is modeled by a matrix.
Not all my readers are mathematically inclined, and I sometimes get polite comments that my posts are too technical, so I’ll explain roughly how a matrix works. Player A listens to player B and responds to the complexity of B’s playing with one of three options: joining player B, ignoring player B, and doing the opposite of player B. We construct a table listing all posssible combinations of player A and player B, and we place a 1, 0, or -1 depending on whether player A follows, ignores, or contrasts with player B, respectively. Note that player A and player B might be the same person, which happens when player A listens to themselves, and this is given by entries along the upper left to lower right diagonal (a.k.a. the main diagonal). The resulting table of entries is our matrix. Here is an example.
| Player B | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| Player A | 1 | 1 | 0 | -1 | 0 |
| 2 | 0 | 0 | 0 | -1 | |
| 3 | 1 | 0 | 0 | 0 | |
| 4 | 0 | 1 | 1 | 0 | |
Each player’s actual decision depends on the sum of the contributions from all the players they are listening to. So for each player A, we look along their row of entries and multiply each matrix entry by each player B’s signal. Sum up all the results, and you have an output signal for each row. This is essentially matrix-vector multiplication. Crucially, the output of the matrix affects the input, producing complex feedback behavior over time. The exact way the output affects the input requires getting into differential equations and will be saved for a later section.
In the model, this matrix is populated randomly with 1’s, 0’s, and -1’s, which creates a wide variety of behaviors ranging from convergence to static values (perhaps drones or ostinati) to oscillations (perhaps call and response). The paper also models the concept of boredom over time, and when the players collectively become too bored, they choose to listen to different people. This is represented by randomizing the matrix again, changing the behavior of the differential equations as they evolve. The result is long-term modulation between static, oscillatory, and sometimes chaotic behavior, which is best shown with a picture. Depicted is a simulation of the CFI Model with four musicians, with moments of matrix re-randomization indicated with vertical dashed lines.
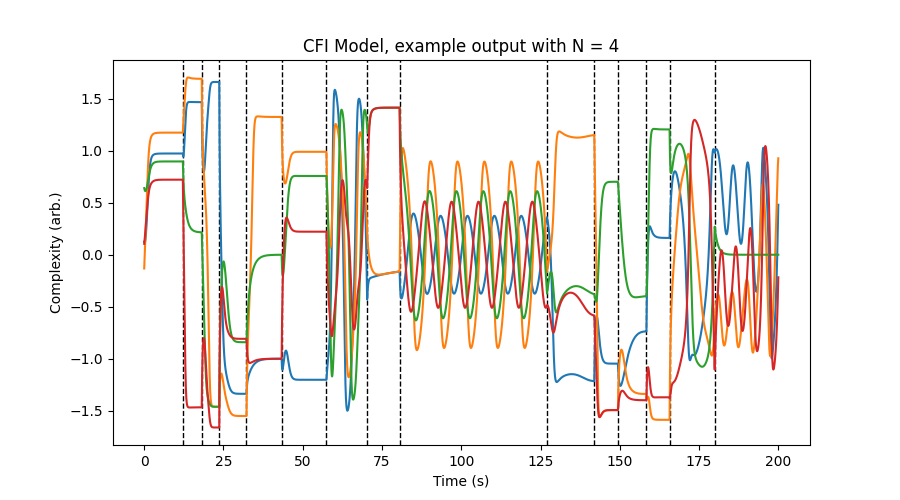
Canonne and Garnier point out that the signal for each player could be made multidimensional with different factors for pitch, rhythm, timbre, etc. This could make the CFI Model suitable for algorithmic music generation (as it is I feel it is a little too simple for that, but read on).
Matrix Modular Synthesis
Having verbosely introduced the Buchla Music Easel and the CFI Model, I can now finally get to the topic of this post. How do these concepts come together? Imagine a set of modules like the Easel (or any other modular synthesizer, really), and then feed every module back into the inputs of every other module in a matrix configuration, with a random matrix that changes over time. I call this Matrix Modular Synthesis, and it is related to the Feedback Integrator Networks concept I discussed a few months ago.
Implementation in SuperCollider is not too hard. The only tricky part is that SuperCollider has no built-in matrix support, so I instead took advantage of its multichannel expansion feature. (If using an alternate language to sclang without multichannel expansion, matrix-vector multiplication can be done with a loop.) Also note LFNoise2.kr(0.5).round as a hacky way of getting random 1’s, 0’s, and -1’s. All the “modules” are based on components of the Buchla Music Easel. The comments should explain the rest.
// Run before booting server.
Server.default.options.blockSize = 1;
(
SynthDef(\easel, {
var snd, numInputs, numOutputs;
numInputs = 12;
numOutputs = 7;
snd = LocalIn.ar(numOutputs);
// Matrix-vector multiplication using multichannel expansion.
snd = snd * ({ { LFNoise2.kr(0.5).round } ! numInputs } ! numOutputs);
snd = snd.sum;
// If additional modules are added, remember to update numInputs and numOutputs.
// numInputs should equal the maximum i in snd[i], plus one.
// numOutputs should equal the number of entries in the snd array.
snd = [
// Oscillator that reaches LFO range
SinOsc.ar(snd[0].linexp(-1, 1, 0.1, 8000)),
// Oscillator in audio range only
SinOsc.ar(snd[1].linexp(-1, 1, 100, 8000)),
// Wavefolder with controllable gain
(snd[2] * snd[3].linexp(-1, 1, 1, 10)).fold2,
// Two filters with controllable cutoff and resonance
MoogFF.ar(snd[4], snd[5].linexp(-1, 1, 10, 8000), snd[6].linlin(-1, 1, 0, 4)) * 3.dbamp,
MoogFF.ar(snd[7], snd[8].linexp(-1, 1, 10, 8000), snd[9].linlin(-1, 1, 0, 4)) * 3.dbamp,
// Metallic reverb (spring reverb in the Easel)
FreeVerb.ar(snd[10], mix: 1),
// Five-step sequencer
Demand.ar(Impulse.ar(snd[11].linexp(-1, 1, 0.1, 1000)), 0, Dseq([-0.1, 0.5, -0.9, 0.3, -0.4], inf))
];
if(snd.size != numOutputs) {
Error("Please ensure numOutputs matches number of modules").throw;
};
snd = Sanitize.ar(snd);
LocalOut.ar(snd);
// Grab output from one of the filters. Try changing the index here, or even using snd.sum.
snd = Limiter.ar(LeakDC.ar(snd[3]));
snd = Pan2.ar(snd, 0);
Out.ar(\out.kr(0), snd);
}).add;
)
Synth(\easel);
Here’s how it sounds – beeps, fizzes, and crackles abound:
The selection of modules heavily influences the aesthetics of the patch. The choice of output signal is also important; options include a single output, a random switch between outputs, or all of the module outputs summed together.
When I was building up this patch, I was surprised at how varied and complex it sounded even with just two oscillators FMing each other.
Although I set SC to use single-sample feedback, the patch also produces good sounds with a standard block size like 64. Try both.
Not all matrices produce acceptable results. Some result in silence. One could analyze the audio output and re-randomize the matrix if an extended period of silence happens. An even more sophisticated patch could use machine listening features on the output and incorporate the boredom model from the paper. Would that sound better than simple randomness? I don’t know, try it.
Matrix Modular Synthesis generates harsh and noisy tones, but with the selection of the right modules it could produce more accessible results. One option worth exploring is quantizing the oscillator frequencies to a scale.
Discussion of the CFI Model
The CFI Model, or rather a simplified version of it, is a system of \(N \geq 1\) ordinary differential equations. \(\mathbf{x}(t)\) is a size-\(N\) vector of signals that vary over time \(t\). Signal \(x_k\) roughly means the complexity of what musician \(k\) plays, with values larger in absolute value meaning more complex musical content. The signals can also be negative, for reasons I don’t fully understand. Let \(\mathbf{\Omega}\) be an \(N \times N\) matrix that indicates which musicians are listening to which, as discussed in a previous section. Then the CFI Model is
where \(\tau_c\) is a constant with time units and \(\mathbf{x}^3\) is computed pointwise. The \(\mathbf{x}^3\) term is ad hoc, and it introduces a nonlinearity that “fights” \(\mathbf{x}\) and prevents solutions from exploding to infinity. Note that \(\mathbf{x}(0)\) must not be all zeros or \(\mathbf{x}\) will be zero forever, so \(\mathbf{x}\) should be kicked off with, say, random values.
The solutions to this system of equations are hard to analyze due to the nonlinearity, but can be tested experimentally with numerical integration. In the case \(N = 1\), if \(\Omega_{11} \geq 0\) then \(x_1\) appears to converge to \(\pm\sqrt{\Omega_{11}}\) provided that \(x_1(0) \neq 0\). If \(N = 2\), a matrix like \(\mathbf{\Omega} = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix}\) results in oscillations as player 1 follows player 2 and player 2 contrasts with player 1. In general, populating \(\mathbf{\Omega}\) with random values of different signs seems to produce convergence, oscillation, or sometimes chaos.
The boredom model (called “boreness” in the paper) is as follows. Define “information” \(I\) as the following scalar signal:
where \(\tau_n\) is another constant with time units. \(I\) is roughly the overall busyness of the music at any moment in time; both high absolute values of \(x_k\) and high rate of change of \(x_k\) contribute toward information, which is always nonnegative.
Define \(b\) or “boredom” as a signal with \(b(0) = 0\). Usually \(b\) grows as \(db/dt = I\), but when \(b\) reaches a constant \(b_\text{max}\), \(b\) is reset to 0 and \(\mathbf{\Omega}\) is re-randomized with entries selected from \(\{-1, 0, 1\}\). These discontinuities technically can make derivatives invalid, but that doesn’t matter much during numerical integration. By the way, I simply used the Euler method to simulate the CFI Model, which is perfectly sufficient for getting the desired behavior.
I am omitting some details where musical events are treated as discrete “clusters” and the signal \(\mathbf{x}\) becomes piecewise constant, as they are not all that important to the model.
Conclusions
Feedback has been a mainstay of sound synthesis for decades, so the true novelty of Matrix Modular Synthesis could be reasonably challenged. However, I think the idea of simulating random live patching with a dynamic matrix adds a new level of control as opposed to manual and fixed feedback setups. It certainly helps that it sounds good, too.