Giorgio Sancristoforo’s recent software noise synth Bentō is a marvel of both creative DSP and graphic design. Its “Generators” particularly caught my eye. The manual states:

Bentō has two identical sound generators, these are not traditional oscillators, but rather these generators are models of analog computing patches that solve a differential equation. The Generators are designed to be very unstable and therefore, very alive!

There’s a little block diagram embedded in the synth’s graphics that gives us a good hint as to what’s going on.

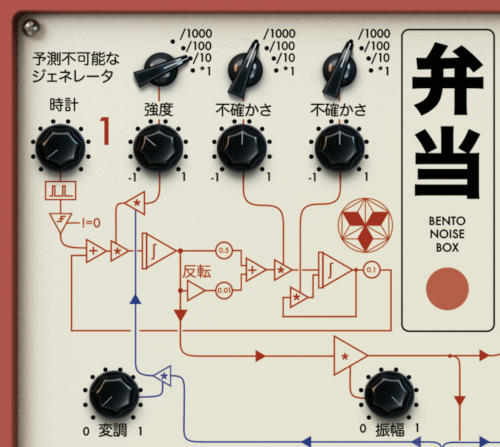
We’re looking at a variant of a state variable filter (SVF), which consists of two integrators in series in a feedback loop with gain stages in between. Sancristoforo adds an additional feedback loop around the second integrator, and what appears to be an additional parallel path (not entirely sure what it’s doing). It’s not possible for chaotic behavior to happen in an SVF without a nonlinearity, so presumably there’s a clipper (or something else?) in the feedback loops.

While thinking about possible generalized forms of this structure, I realized that the signal flow around integrators can be viewed as 2 x 2 feedback matrix. A form of cross-modulation across multiple oscillators can be accomplished with a feedback matrix of greater size. I thought, why not make it like a feedback delay network in artificial reverberation, with integrators in place of delays? And so a new type of synthesis is born: the “feedback integrator network.”

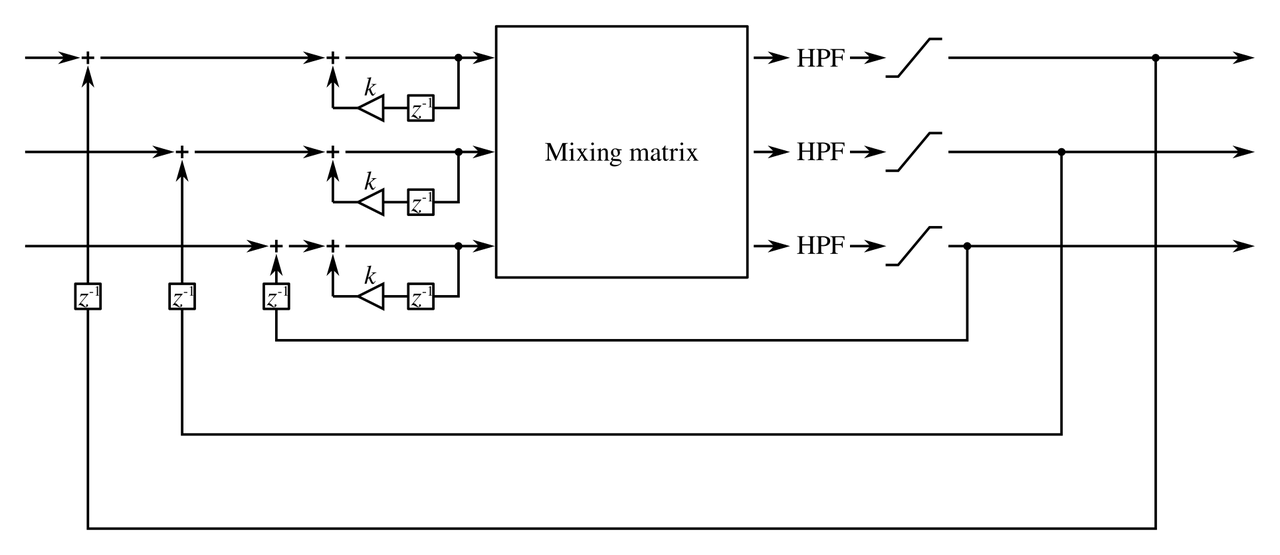
An N x N feedback integrator network consists of N parallel signals that are passed through leaky integrators, then an N x N mixing matrix. First-order highpass filters are added to block dc, preventing the network from blowing up and getting stuck at -1 or +1. The highpass filters are followed by clippers. Finally, the clipper outputs are added back to the inputs with single-sample delays in the feedback path. I experimented with a few different orders in the signal chain, and the order presented here is the product of some trial and error. Here’s a block diagram of the 3 x 3 case:

A rich variety of sounds ranging from traditional oscillations to noisy, chaotic behavior results. Here are a few sound snippets of a 8 x 8 feedback integrator network, along with SuperCollider code. I’m using a completely randomized mixing matrix with values ranging from -1000 to 1000. Due to the nonlinearities, the scaling of the matrix is important to the sound. I’m driving the entire network with a single impulse on initialization, and I’ve panned the 8 parallel outputs across the stereo field.

// Run before booting server.
Server.default.options.blockSize = 1;

(
{
    var snd, n;
    n = 8;
    snd = Impulse.ar(0);
    snd = snd + LocalIn.ar(n);
    snd = Integrator.ar(snd, 0.99);
    snd = snd * ({ { Rand(-1, 1) * 1000 } ! n } ! n);
    snd = snd.sum;
    snd = LeakDC.ar(snd);
    snd = snd.clip2;
    LocalOut.ar(snd);
    Splay.ar(snd) * 0.3;
}.play(fadeTime: 0);
)

The four snippets above were not curated – they were the first four timbres I got out of randomization.

There’s great fun to be had by modulating the feedback matrix. Here’s the result of using smooth random LFOs.

I’ve experimented with adding other elements in the feedback loop. Resonant filters sound quite interesting. I’ve found that if I add anything containing delays, the nice squealing high-frequency oscillations go away and the outcome sounds like distorted sludge. I’ve also tried different nonlinearities, but only clipping-like waveshapers sound any good to my ears.

It seems that removing the integrators entirely also generates interesting sounds! This could be called a “feedback filter network,” since we still retain the highpass filters. Even removing the highpass filters, resulting in effectively a single-sample nonlinear feedback delay network, generates some oscillations, although less interesting than those with filters embedded.

While using no input sounds interesting enough on its own, creating a digital relative of no-input mixing, you can also drive the network with an impulse train to create tonal sounds. Due to the nonlinearities involved, the feedback integrator network is sensitive to how hard the input signal is driven, and creates pleasant interactions with its intrinsic oscillations. Here’s the same 8 x 8 network driven by a 100 Hz impulse train, again with matrix modulation:

Further directions in this area could include designing a friendly interface. One could use a separate knob for each of the N^2 matrix coefficients, but that’s unwieldy. I have found that using a fixed random mixing matrix and modulated, independent gain controls for each of the N channels produces results just as diverse as modulating the entire mixing matrix. A interface could be made by supplying N unlabeled knobs (likely less) and letting the user twist them for unpredictable and fun results.