Vintage synth hacker and generative electronic music producer acreil, a.k.a. Scott Nordlund, posted a video breaking down a PD patch he made. Go watch it now. Of the delightful DSP tricks to be found within, the most delightful to me is his review of the Casio CTK-1000, and the unearthing of its synthesis method.

The Casio CTK-1000 is a 1993 sythesizer and rompler whose manual boasts a new type of synthesis called “IXA Sound Source,” distinguished from phase distortion synthesis from the CZ series and “interactive phase distortion” or iPD from the Casio VZ series. These are largely ways of getting around Yamaha’s all-dominating FM synthesis patents.

Nordlund dug up Casio’s patent US5164530, and while we have no way of telling what’s really inside the CTK-1000, the document gives us useful clues. (There are three other patents, but none of them seem to contain much interesting information beyond this one.) The patent describes a phase modulation synthesis method where the carrier is a triangle wave and the modulator is a sine wave. However, the intrinsic phase of the triangle wave is distorted with a weird waveform made of sine wave segments such that a sine wave is produced if the modulation index is zero. Here’s a block diagram:

and a closer look at the weird waveform:

For readers who prefer a more formal description, define a pulse wave \(\Pi_x(t)\) as a function with period \(x\) such that \(\Pi_x(t) = 1\) if \(0 \leq t < x / 2\) and \(\Pi_x(t) = 0\) if \(x / 2 \leq t < x\). Define a triangle wave \(\Delta(t)\) as a function with period \(4\) such that

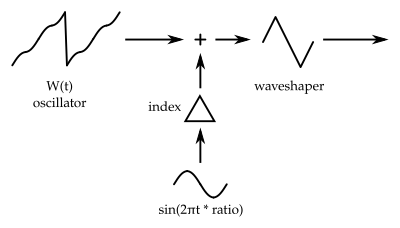
Then the weird waveform \(W(t)\) with period \(1\) is defined as:

An IXA oscillator with period \(1\), index \(n\), and ratio \(r \in \mathbb{N}\) is defined as:

It can be seen that \(\text{IXA}(0, r, t) = \sin(2 \pi t)\), i.e. turning off the modulator results in a sine wave.

IXA synthesis, as it could be called, produces unique buzzy waveforms with a deep and growly sound even with low index:

It sounds a bit like wavefolding. Classic two-operator sine wave FM, by comparison, sounds more muted when the index is low and squelchy when the index is high:

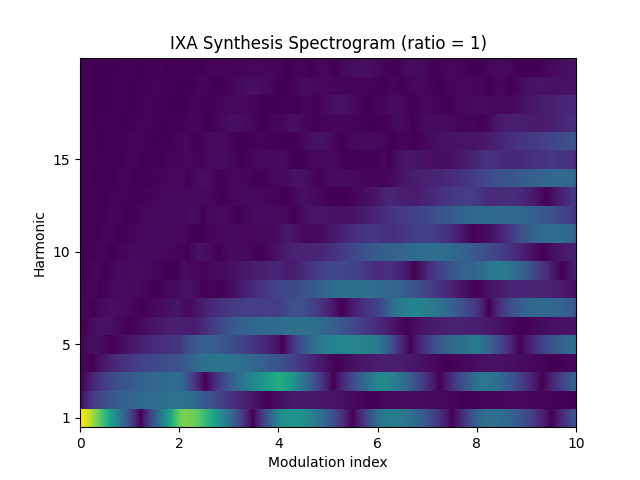
Here’s a spectrogram of partials for IXA with ratio set to 1:

Here is two-operator FM synthesis with sine waves for comparison. Note the change of scale in the X-axis – FM requires a higher modulation index to achieve sounds comparable in brightness to IXA.

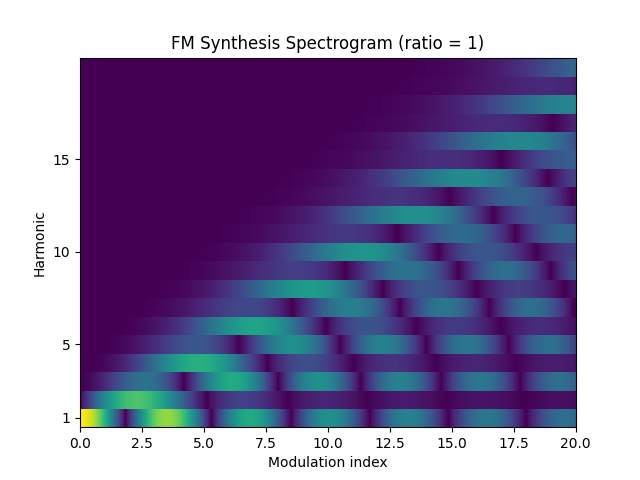
The amplitude scale is linear in both graphs. Notice how the FM synthesis, whose harmonics follow one of the Bessel functions, has a sort of “resonance” at increasing even harmonics and quickly drops off to near-zero above that. IXA synthesis produces smoother spectra with less obvious resonance, and if you look closely there is some high-frequency fuzz above the dropoff.

IXA also works with non-integer ratios, but to me these sound harsh, like a bell FM patch run through nonlinear distortion:

Slight detuning of the modulation frequency, however, produces a pleasant beating effect.

The patent also touches on some variations. One is to pick a different \(W(t)\) so it no longer produces a sine wave when the modulation index is zero. I have experimented with this a little, but haven’t gotten anything good out of it. Another, more interesting, option is to open up the modulator to be the output of another IXA synthesis oscillator, or the output of the current oscillator in a feedback configuration. Chaining two or three IXA oscillators seems to automatically produce brostep bass waveforms, but I’m not sure if it’s useful for much else:

The way I see it, three or more operators are useful in FM to access richer sounds, but a single IXA operator is already complex enough and additional operators are limited in use.

Generally, anywhere FM or PM is used, it’s worth trying to substitute IXA to see how it sounds. For example, IXA produces formant-like results when setting a high modulation ratio, so FM vocal synthesis may apply to IXA as well.

// Public Domain

(
var ixa;

ixa = { |freq, in, index|
    var phase, waveform, snd;
    phase = Phasor.ar(Impulse.ar(0), freq / SampleRate.ir, 0, 1);
    waveform = (phase % 0.5 * 2pi).sin * (2 * (phase % 0.5 < 0.25) - 1);
    waveform = waveform + (2 * (phase % 0.5 >= 0.25));
    waveform = waveform + (2 * (phase >= 0.5));
    snd = (waveform + (in * index)).fold2;
    snd;
};

{
    var freq = 100;
    ixa.(freq, SinOsc.ar(freq), Line.kr(0, 10, 3)) * 0.5 ! 2;
}.play(fadeTime: 0);
)