DM Synthesis
A while back, I tried recreating the sound of a dialup modem from scratch, which involved a dive into multiple PDFs of telecommunication standards. (I am not the first person to do this.) Very helpful was Windy Tan’s beautiful analysis breaking down a spectrogram of a real dialup handshake. A particularly famous bit is the nasal mid-low “whine” at the end of the handshake, and if you’ve ever wondered what that is, you’re hearing line probing signals L1 and L2, which are synthesized using additive synthesis. The exact partial frequency, phases, and amplitudes are specified in section 10.1.2.4 of ITU-T V.34. They’re at 9 seconds in this recording of a modem by thearchiveguy99 on Freesound:
WARNING: Audio files in this post are loud and piercing. Please turn up your speakers to extremely painful levels for optimal telecommunication.
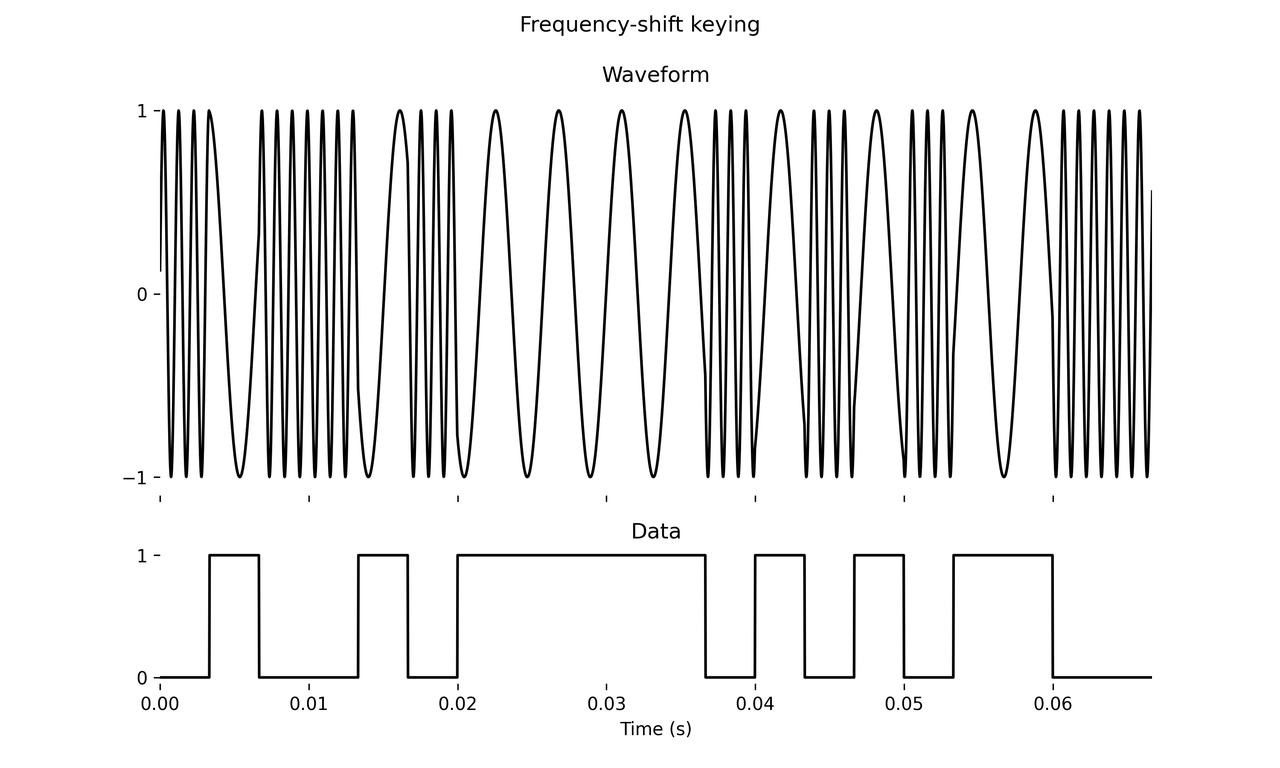
The whine is legendary, but I want to turn your attention to high-frequency gurgles before it, starting at about 4 seconds in, some of them resembling slurping a last bit of soda through a straw in a McDonald’s cup. These tones, specified at a high level in ITU-T V.8bis, are encoded using frequency-shift keying (FSK) as given in the lower-level ITU-T V.21 spec. In its simplest form, FSK uses a single sine wave to encode a binary signal by modulating its frequency. Following V.21’s description of a “channel 1” signal, at regular intervals of 1/300 seconds, a single bit is transmitted. If the bit is 0, the sine wave’s frequency is set to 1180 Hz. If the bit is 1, the frequency is set to 980 Hz.
Yep, that’s a dialup gurgle. The graph below demonstrates this visually (for different parameters — I had to lower the carrier for the 1 bits so that the distinction between the two is obvious). Above we have the audio waveform, below it the data signal.
Designing that dialup imitation made me realize that I really like how FSK sounds purely as a sound design tool. This got me looking into its various siblings, which are known as the “digital modulation” schemes for transmission of digital signals over an analog medium such as radio. In contrast, in “analog modulation” the signal being transmitted is continuous, encompassing familiar techniques like FM, AM, and single-sideband modulation. Today we’re going to honor the long tradition of adapting telecommunications methods for creative use by seeing what kind of sounds we can design by directly listening to signals produced with FSK and related methods. I call this approach Digital Modulation Synthesis, a name I’m not in love with, but I couldn’t think of a better one. It may be abbreviated to the cooler-sounding “DM Synthesis.”
In telecommunications, modulation is only half the story, and you also need a demodulator which takes the transmission signal and gets the data back. Engineering modulators and demodulators in a way that’s robust to noise is an interesting problem subject to nearly a century of study, but here we’re going to be the weirdos who just want to listen to the modulated signal itself. I will spend no time here discussing the engineering tradeoffs of these digital modulation schemes in a telecommunication settings; those problems are very interesting and deep but not relevant to this post.
This post is pretty light on math, and the DSP isn’t fancy here, as our concentration is more on sound design and synthesis. All this should be doable in SuperCollider, Pd, Max, etc. with pre-existing units.
I didn’t research this post as thoroughly as I would have liked, so it’s not impossible that I have misrepresented things from the telecommunications literature. If there are mistakes, sorry about that.
On-off keying (OOK)
To introduce some terminology, our digital modulation schemes will have at least one carrier frequency which is just the frequency of the synthesized oscillator, and a signaling rate which is the number of bits per second. The reciprocal of the signaling rate, and therefore the time interval between bits, is notated \(T\) and given in seconds. In our above example, \(T = 1/300\).
Probably the simplest form of digital modulation is on-off keying (OOK), which encodes a binary signal by turning a sine wave on or off. You start by synthesizing a sine wave at the carrier frequency, and every \(T\) seconds, set the amplitude to either 1 or 0 as determined by the input bit.
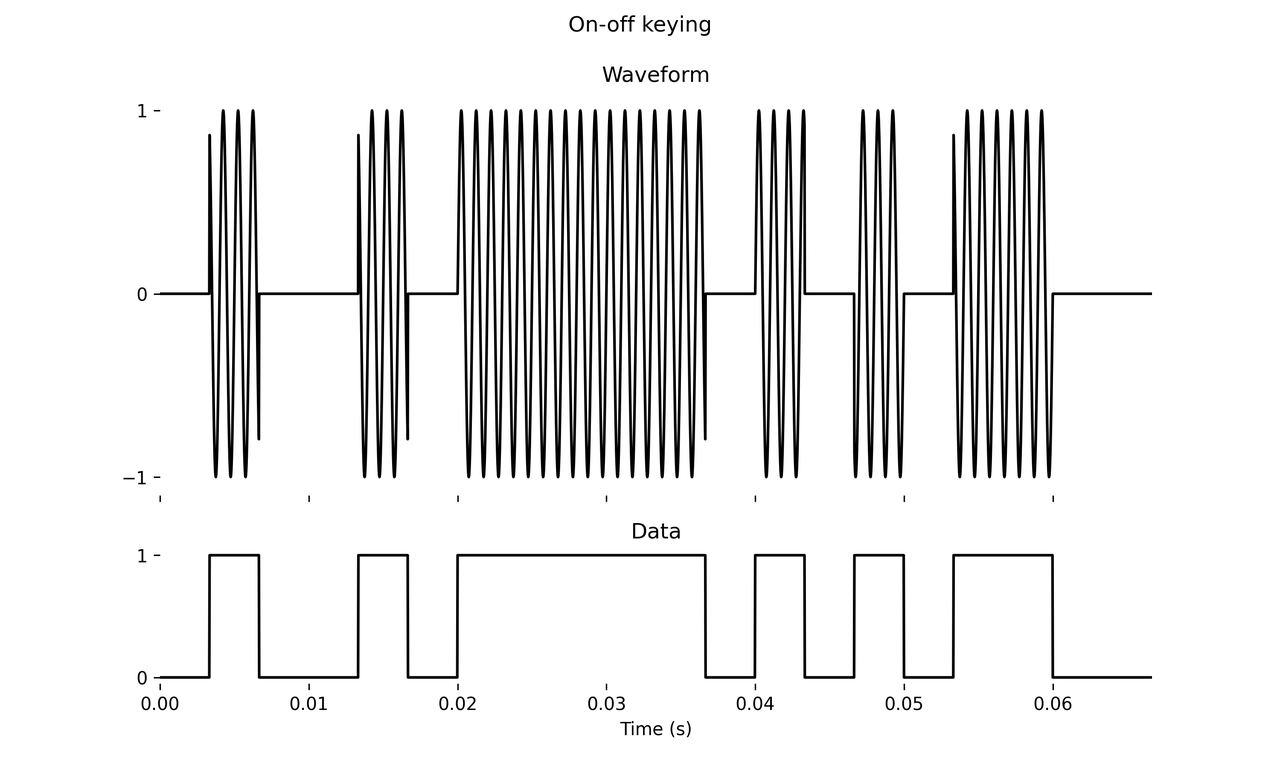
Here I’ve set the carrier frequency to 1000 Hz and the signaling rate to 300 Hz. The modulation parameters available to us are the carrier frequency and signaling rate. In particular, the ratio between them is of importance; if the carrier frequency is an integer multiple of the signaling rate, then the sine wave will always resume at the same phase. (This is directly analogous to inharmonic vs. harmonic FM synthesis.) OOK has a pretty harsh sound here due to discontinuities in the final signal; you can also add some smoothing to the on-off transitions if you want to change that.
This is a good time to discuss the input bit stream. This is art, so we have the liberty of making up whatever data we want:
An independent random choice for each bit. The probability could be 50% or controlled as a synthesis parameter.
A periodic bitstream, like 0, 1, 1, 0, 1, 1, 0, 1, 1, … These are audibly different from aperiodic signals.
Some mathematical pattern like the Thue-Morse sequence, Fibonacci word, characteristic functions of any integer sequence, etc.
A random bit stream but the probabilities are non-independent, e.g. Markov chains.
1-bit audio signal from anywhere.
Raw data from somewhere else, such as ASCII text or a random file you have sitting around.
Switching among any subset of the above.
Amplitude-shift keying (ASK)
OOK is a special case of amplitude-shift keying (ASK), where instead of just amplitudes 0 and 1 you can have any fixed number of amplitudes. As such the input signal is no longer a bit stream, but a discrete signal with a fixed number of values.
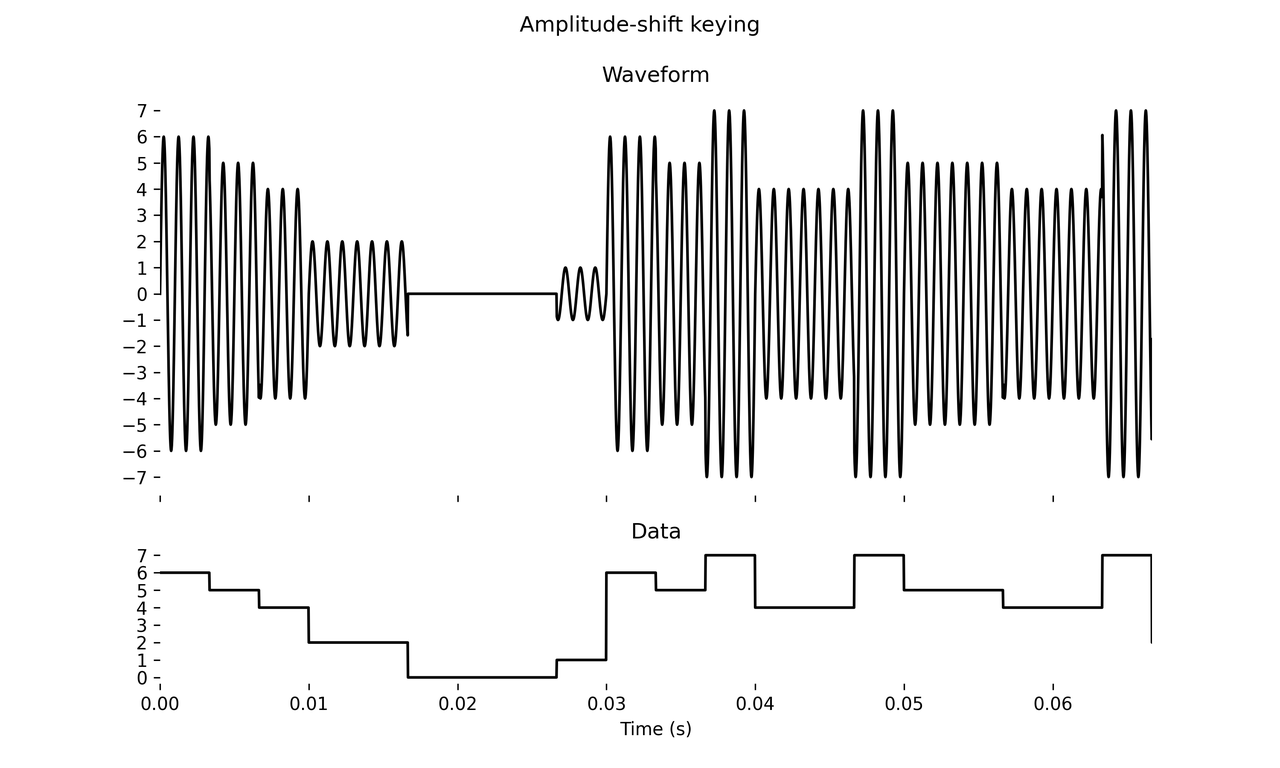
Here, the data signal takes on eight evenly spaced values from 0 to 7 inclusive, with values streamed with a 300 Hz frequency. The carrier is 1000 Hz again.
Frequency-shift keying (FSK)
I have already introduced FSK, which modulates a bit stream using a single sine wave that jumps between two carrier frequencies depending on the input bit. Let’s see that again. (Again the image and audio do not match here; I spaced the carriers in the graphic farther apart for visual clarity.)

To clarify, the transitions between the frequencies are immediate, but the sine wave’s phase is continuous and the jumps do not actually create a discontinuity in the signal. As such, FSK is essentially FM synthesis where the modulator signal is 1-bit.
FSK vowel synthesis: Since it generates two frequency peaks, FSK can be used as a formant synthesizer. The human ear is incredibly sensitive to audio with speech-like qualities, and in my experience only needs to hear two formants moving in opposite directions in the 500-3000 kHz range to start getting the impression of something vocal. Long ago I learned that you can make extremely bright growls by FMing a sine wave with a square wave and messing with the modulation index so that the sine wave alternates between two frequencies that move in opposite directions. Here’s what that sounds like with the data signal at 100 Hz, the lower frequency sliding from 500 to 800 Hz, and the upper one sliding from 2000 Hz to 1000 Hz:
The FSK generalization of this is that now the alternation between the two carrier frequencies is controlled by an arbitrary bit stream. Here’s the same idea with random bits (I raised the data signal rate to 300 Hz since it just sounded better):
If you need more formants, you can either mix together multiple FSK instances, or use three or more frequencies (see next section).
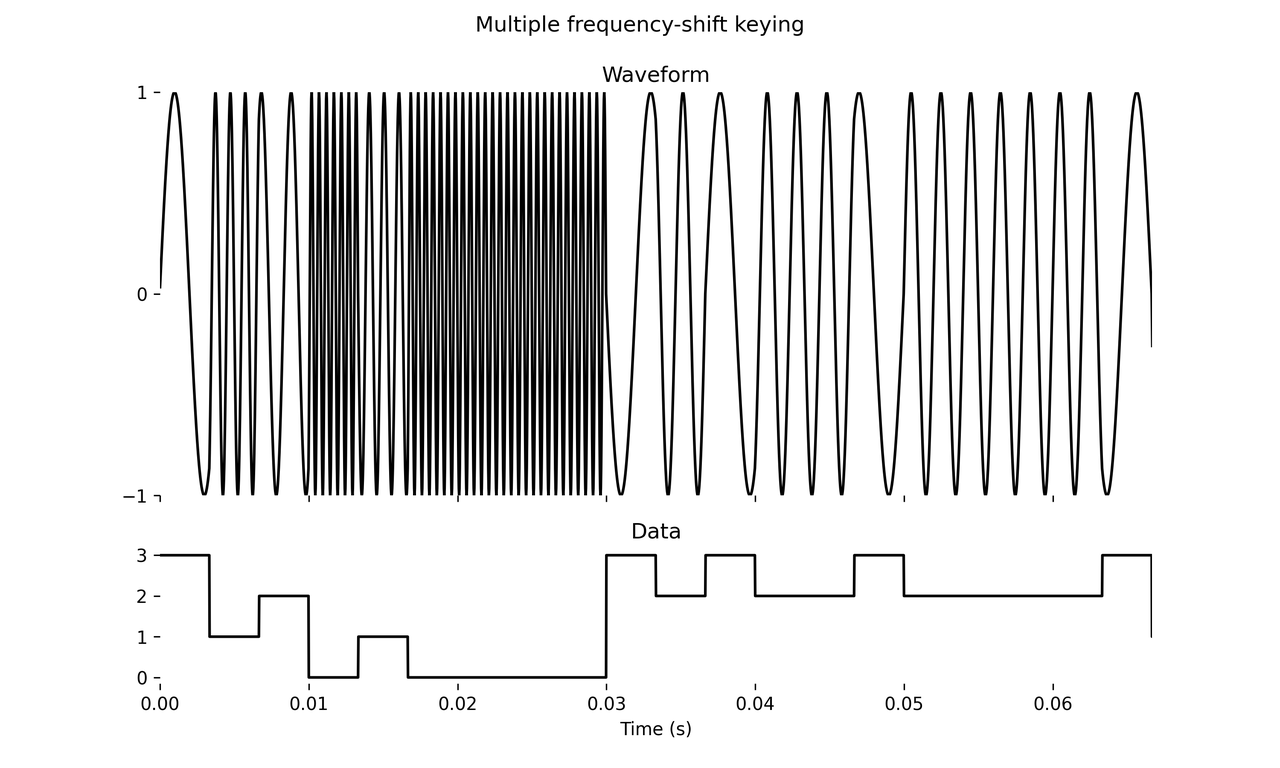
Multiple frequency-shift keying (MSFK)
FSK usually refers to only two carrier frequencies, but you can use as many as you want to modulate an integer signal with 3 or more discrete values. While straightforward to explain, consider the musical options — you can tune these frequencies to vocal formants, or to a scale or chord, or harmonics of a fundamental, or to peak frequencies analyzed in an input signal. I’ve just used 4 stacked octaves with the bottom one at 250 Hz for this example.
Binary phase-shift keying (PSK)
Phase-shift keying methods use only a single carrier frequency, synthesized with a sine wave, but its phase is modulated in response to the input signal.
There are two ways to think of binary phase-shift keying (BPSK). One way to think of it is as flipping the carrier sine wave’s phase by 180 degrees for 1 bits. That is, the signal is synthesized as \(x = \sin(2\pi f_c t + \phi(t))\), and every \(T\)-second interval, if the input bit is 0 then set \(\phi(t) = 0\); if it is 1 then set \(\phi(t) = \pi\). Alternatively, BPSK is ASK where the two amplitudes are \(\pm 1\). That is, the signal is synthesized as \(x = A(t) \sin(2\pi f_c t)\), and every \(T\)-second interval, if the input bit is 0 then set \(A(t) = 1\); if it is 1 then set \(A(t) = -1\). These are equivalent.
It seems most common for the signal period \(T\) to be an integer multiple of the carrier’s period \(1/f_c\), so I have here set \(T = 4/f_c\).
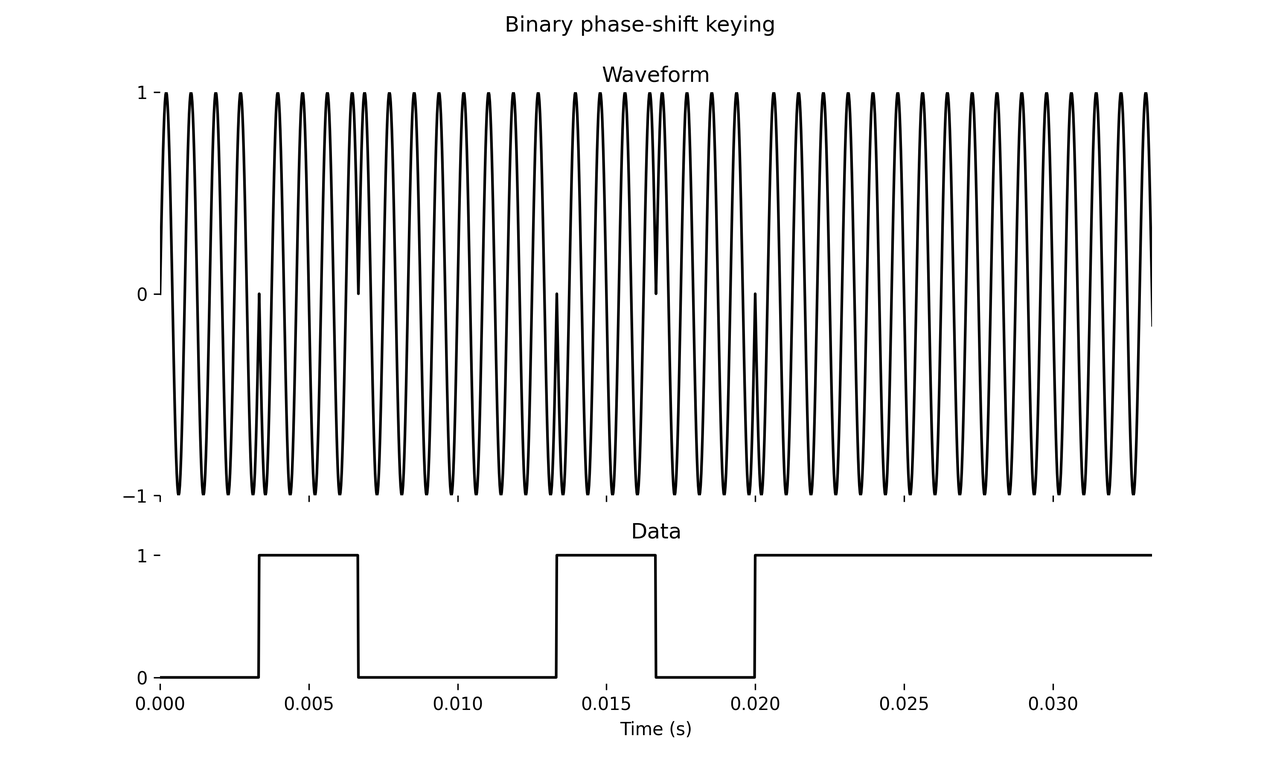
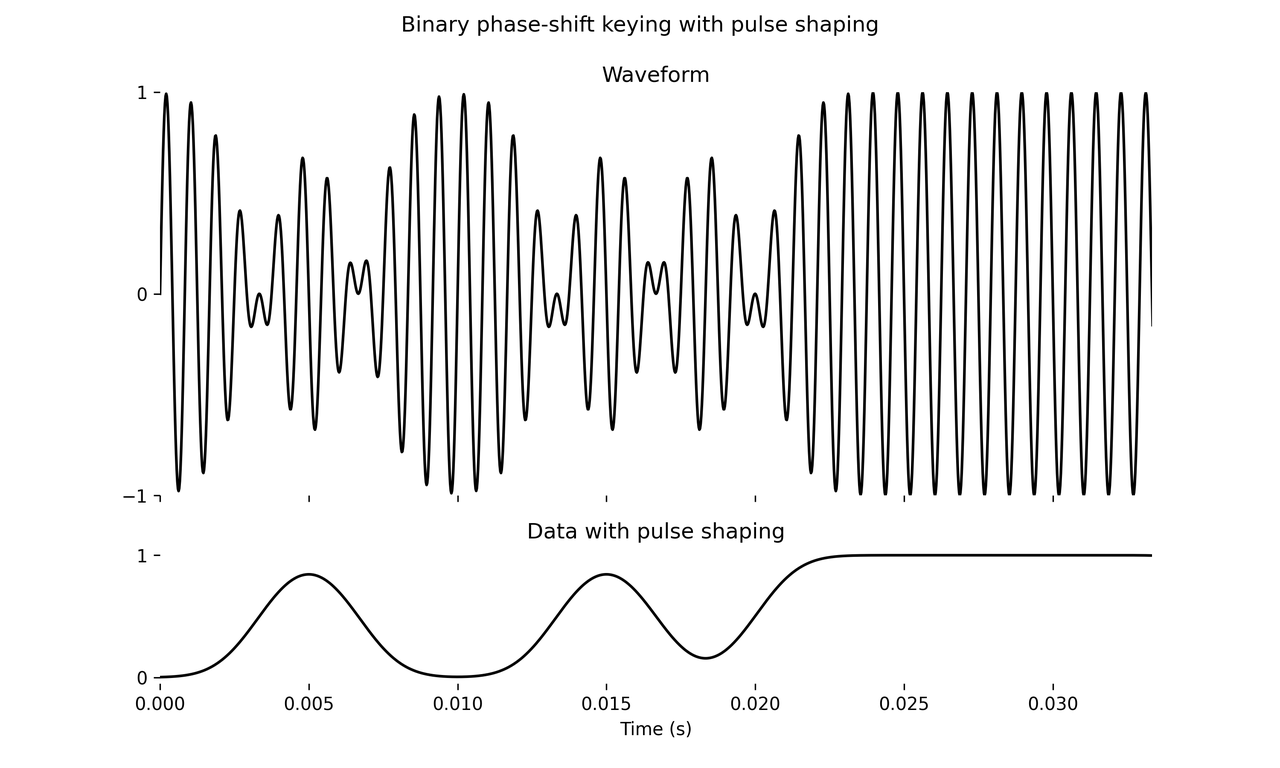
It is common to smooth out the modulation signal using a lowpass filter prior to modulation. [1] This is “pulse shaping” (although I am oversimplifying since pulse shaping is actually done on an impulsive signal rather than the “latched” one we use here, see [2]). To my understanding, pulse shaping of BPSK is always done in the “ASK domain” by filtering the amplitude signal \(A(t)\), not the phase signal \(\phi(t)\).
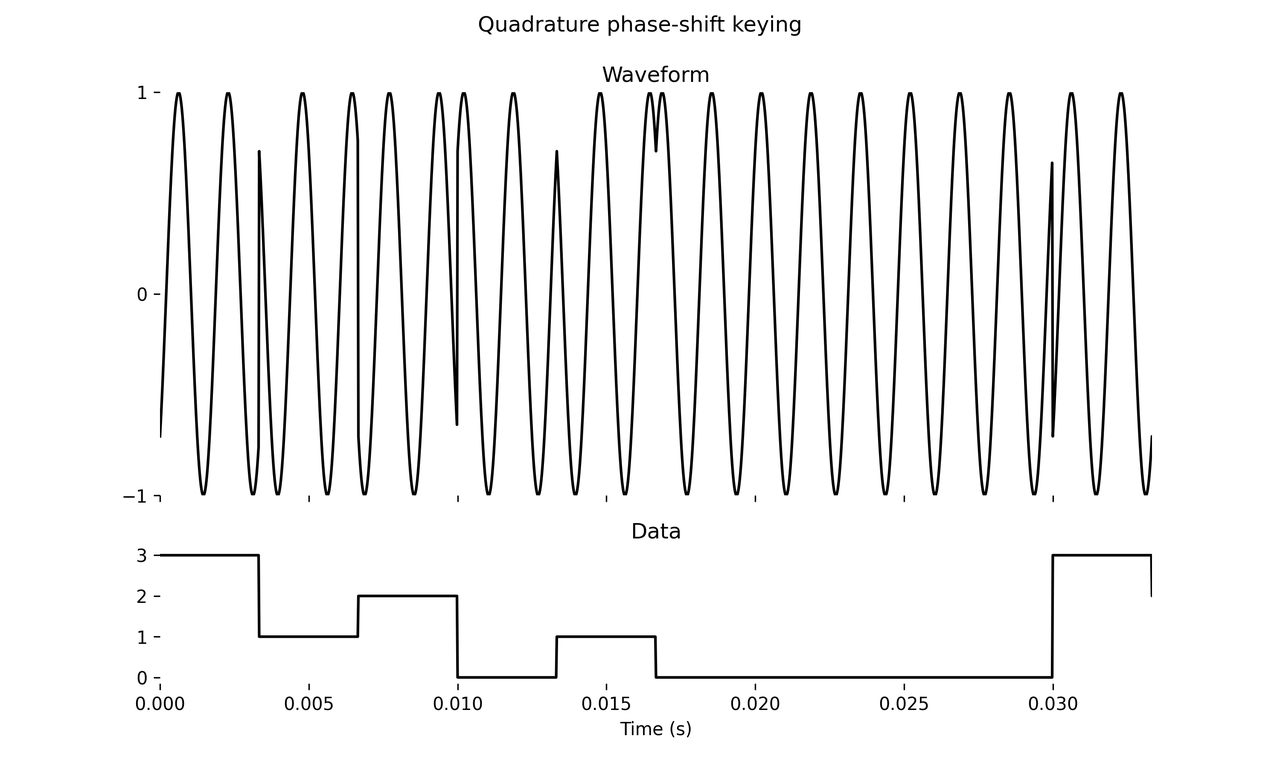
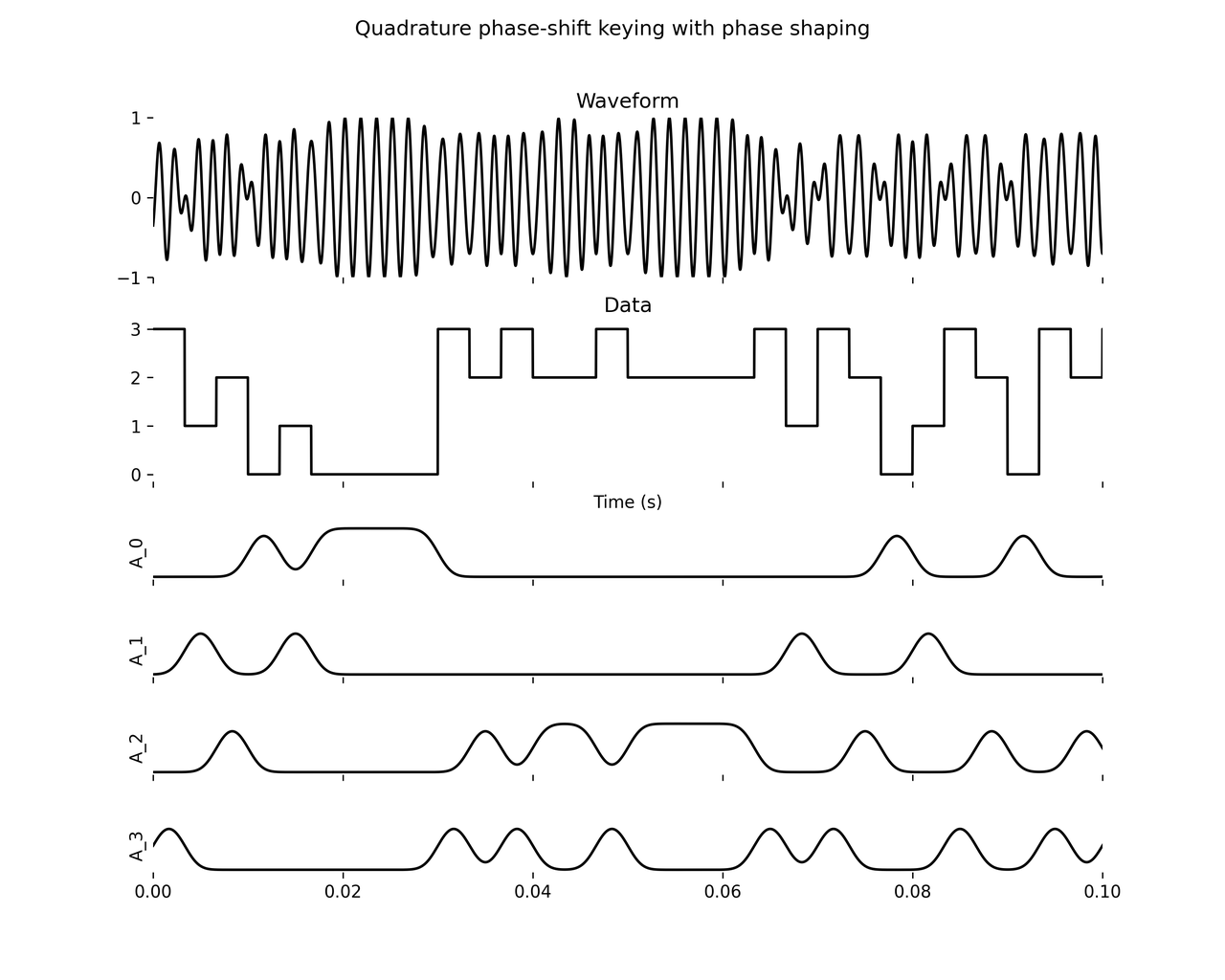
Quadrature phase-shift keying (QPSK)
In quadrature phase-shift keying (QPSK), the input signal is no longer binary but has four different values. Let’s say the input signal is \(b(t)\) which takes on values 0, 1, 2, or 3 and is piecewise constant at intervals of \(T\) seconds. We use four sine waves spaced at 90-degree phase offsets and multiplex them:
where \(A_0(t)\) is set to 1 whenever \(b(t) = 0\) and set to 0 otherwise, and \(A_1(t)\) is set to 1 whenever \(b(t) = 1\) and 0 otherwise, and so forth. Effectively this is multiplexing the four sine waves, and only one is on at a time. You can also write all this with phase modulation where the phase offsets may only take on values \(\pi/4, 3\pi/4, 5\pi/4, 7\pi/4\), but we’ll see why the above is better in a moment.
As with all PSK schemes, sources recommend \(T\) being a multiple of \(1/f_c\). In these examples I have set \(T = 2/f_c\).
Offset quadrature phase-shift keying (OQPSK) is a further variant of QPSK with the constraint that the phase may only jump in 90-degree increments. That is, \(b(t)\) may not jump directly between 0 and 2 or between 1 and 3. So in reality, each interval is encoding a single bit – as each sample \(b(t)\) either steps up or down by 1 (modulo 4).
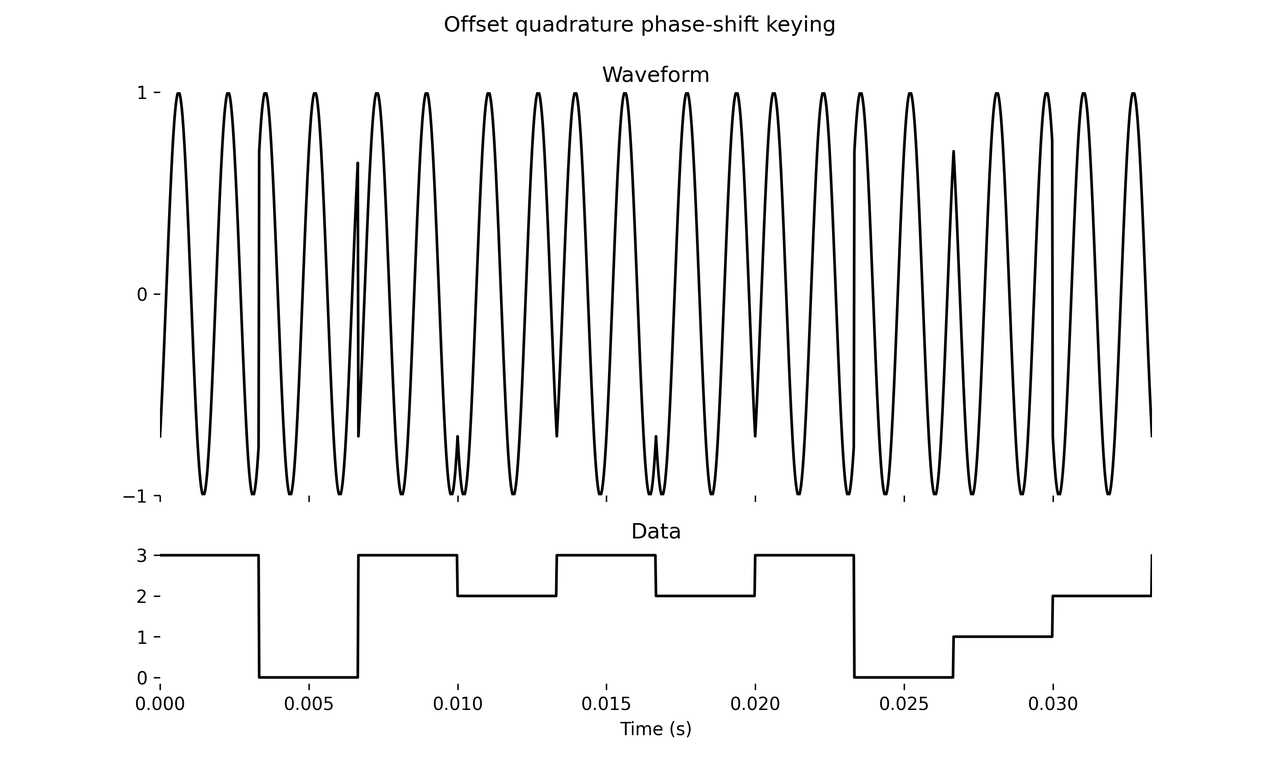
It doesn’t sound or look radically different but I swear it’s a little smoother to the ears. One way to synthesize the phase signal in a modular-like environment is to sum two 1-bit signals, each with a signaling rate of \(2T\) and one of them delayed in time by \(T\).
It is also common to pulse-shape QPSK. The way to do so is to filter the four amplitude signals \(A_i(t)\) with the same lowpass filter. Here, below the waveform and the data signal, I’ve plotted these four signals.
Miscellany
This isn’t the full gamut of digital modulation techniques that have appeared in the literature. I’ve left off Gaussian Frequency-Shift Keying (GFSK) which is FSK with a lowpass filter on the modulator, the various other PSK variants like 8-PSK or \(\pi/4\)-PSK, and the digital variant of Quadrature Amplitude Modulation (QAM). But it’s enough to get some cool sounds, I figure.
(Minimum-shift keying or MSK is just a special case of FSK, and DPSK appears to be a preprocessing stage, so nothing too interesting for sound design applications.)
Instead of piling on more established methods, I’ll throw in some wilder ones that we have the freedom to do in a synthesizer:
In all of these methods, the sine wave carrier can be swapped out for a non-sine-wave carrier.
In FSK-like methods, the “carrier” can be not an oscillator but the cutoff of a filter.
In methods like BPSK/QPSK/OQPSK, in the absence of pulse shaping, you can think of them as sequencing (say) 4 different sinusoids depending on the input data. Instead of using 4 different sinusoids of different phases, try 4 arbitrary segments of audio sourced from anywhere.
Discussion
I have felt that a lot of writing on this blog has lacked good visual aids to explain DSP algorithms. The main reason is that I’m lazy and it really takes a lot of work to make them. Hopefully the amount of effort here pays off, even for these fairly simple DSP algorithms. I would liked to have added some block diagrams to demonstrate how to implement these in synthesizers, but unfortunately I don’t have the energy for that now.
I mentioned in the intro that there’s a long history of creative music DSP arising from telecommunications. That’s an understatement, because the entire field of signal processing basically originated from people designing communication systems, and most effects used in music production originated in that field. FM synthesis of course developed from FM radio, but we also have frequency shifters using tech from SSB radios. The first vocoder, SIGSALY, was developed for the military. Analog filters first found practical use in telegrams.
I can envision four different broad approaches for employing codecs in musical applications:
Type 1: data → encode as an audio signal.
Type 2a: input audio → encode → decode.
Type 2b: input audio → encode → add noise or other effects → decode.
Type 3: input audio → decode as another audio signal.
Type 4: input audio → decode to some signal → encode as audio signal.
Here I’ve explored type 1. Types 2a and 2b would describe things like bitcrushers (there’s a surprising number of ways to bitcrush audio, possibly the subject of a future post), linear predictive coding, or audio effects that simulate MP3 artifacts – you encode the signal, usually in some lossy way, and then decode it. Types 3 and 4 would involve demodulating audio signals that were not necessarily intended to be demodulated.