Cybernetic Synthesis and Roland Kayn

Let’s open this post with music. If you aren’t familiar with the late composer Roland Kayn’s work, listen to one of his Electronic Symphonies, or at least sample a few minutes. The album cover links to his official Bandcamp.
I found out about Kayn’s music through a thread on Lines, and it gets only more interesting as I looked into his story. Kayn was an exponent of combining music with cybernetics, a field I gloss as “the study of feedback systems.” At its heart, it’s a mathematical study; Norbert Wiener’s original text Cybernetics is chock full of integrals and differential equations. As the field developed, it overlapped significantly with medicine, social sciences, humanities, and especially critical theory. I do hope to read Wiener’s Cybernetics and The Human Use of Human Beings, but haven’t gotten around to them, so consider my understanding of the field surface-level — I’m mainly concerned with cybernetics as it relates to Kayn’s music.
Kayn began making cybernetics-influenced electronic works in university electronic music studios in the 60’s. We don’t know what exact tools, but Pickles’ 2016 dissertation Cybernetics in music surmises that the equipment back then was something along the lines of tape machines and basic analog processors and generators: oscillators, noise, filters, reverbs, envelope generators, ring modulators. More intriguingly, recordings of his works were entirely real time — a stark contrast to the offline tape-based processes of the contemporary musique concrète movement. Critic Frans van Rossum wrote in 2011 that Kayn worked with a “network of electronic equipment” and a “a system of signals or commands that it can obey and execute” (quote also via Pickles).
EDIT 2023-12-20: An earlier version of this post credited the technology to Kayn alone, but I have since been properly schooled: it was Jaap Vink who actually built the system, as Sascha Frere-Jones wrote in 4Columns. Given the intimacy that cybernetic musicians necessarily have with their tools, his fingerprints are deeply embedded in Kayn’s electronic works. The sources I looked at didn’t make this clear to me, and most don’t even mention Vink by name. Vink referred to himself as a technician, not a composer, and it’s possible that the concealment of his status was his preference.
That these works were likely made on 60’s equipment, were recorded in real time, and sound varied and dynamic over long stretches of time should impress anyone familiar with modular synths. The implications that his musical systems had some kinds of self-generating and autonomous properties makes this even more remarkable. Now Kayn’s output is more than just great music, it’s now a puzzle. How did he make this music? Can we recreate part of his process?
I don’t think we’ll ever get definitive answers. Kayn died in 2011, Vink in January 2023. While there’s a small body of writing about them, little of it is technical. We can only guess, but we have some resources that helps us with the guessing process — the Lines thread I mentioned, and also La Synthèse Humaine, a YouTube channel run by musician Émile Zener a.k.a. Gunnar Haslam. He takes direct inspiration from Kayn, and unlike me has extensively studied the cybernetics literature. I won’t take the time to resummarize the Lines thread or Zener’s work — just go check them out for yourself — instead I am interested in expanding on them.
Making a cybernetic LFO
It’s perhaps easiest if I first walk you through a concrete example of building a cybernetic patch. We begin with the simple harmonic oscillator, which can be implemented with the system of ordinary differential equations
and the following block diagram:
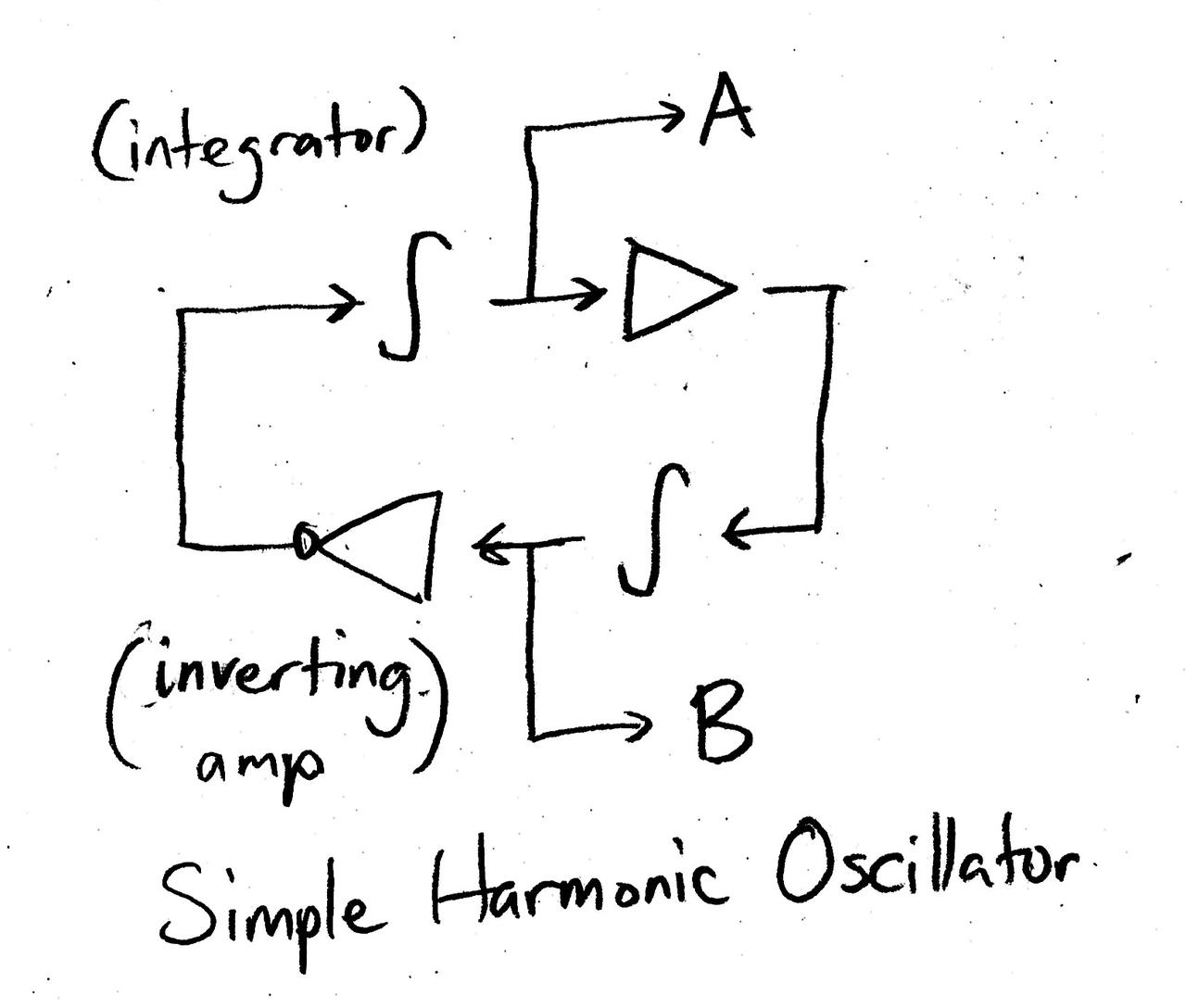
This comprises two integrator stages in a feedback loop. An integrator is a unit that continuously accumulates the input signal (you can get something like a leaky integrator with a one-pole lowpass filter with a very low cutoff). The triangles are simple amplifiers multiplying by constants; one must be negative and the other positive. There are two outputs, A and B, which produce a sine and cosine wave respectively. The system does need an initial “kick” to generate sine waves, by e.g. initially setting \(a(0) = 1\) and \(b(0) = 0\).
Assume that the oscillator is tuned to oscillate at a slow 1 Hz. It is an “LFO” in the literal sense that it oscillates at a low frequency, but critically we aren’t generating it with an actual oscillator module, and the oscillation is an emergent property of the system that we built. We can turn this into an audible synthesis patch by using the two outputs, A and B, as amplitudes, multiplying them with VCAs by two saw oscillators with static frequencies. Mixing the oscillators together, we have a simple looping alternation between two “notes” even though we have no actual sequencer here.
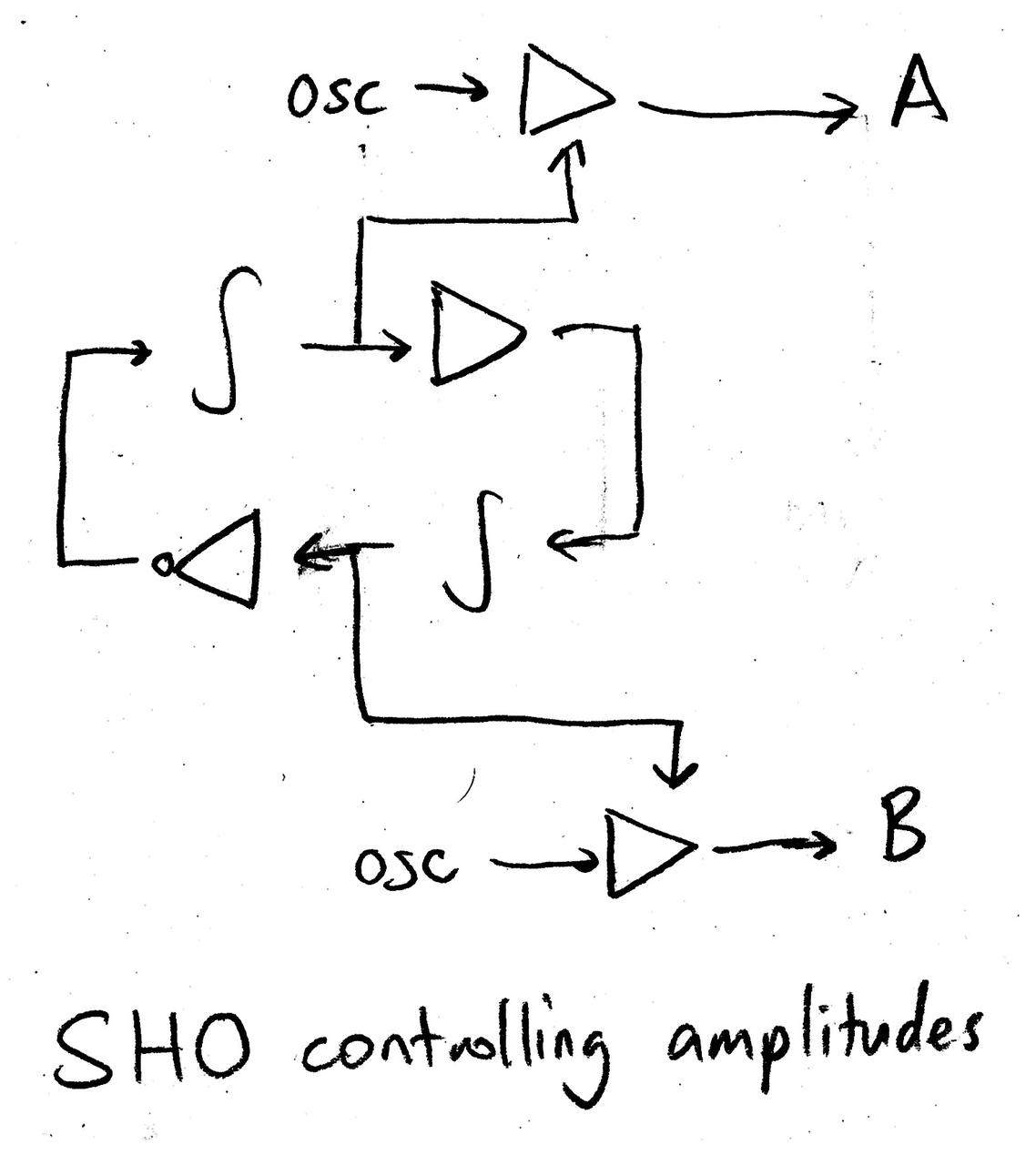
However, the oscillators and VCA’s aren’t part of a loop, and their output does not influence the rest of the system. For reasons that I’ll justify later, we loop in their VCAs by running an envelope follower on the output of the VCAs, and using it to modulate the coefficients of other VCAs that are in the loop.
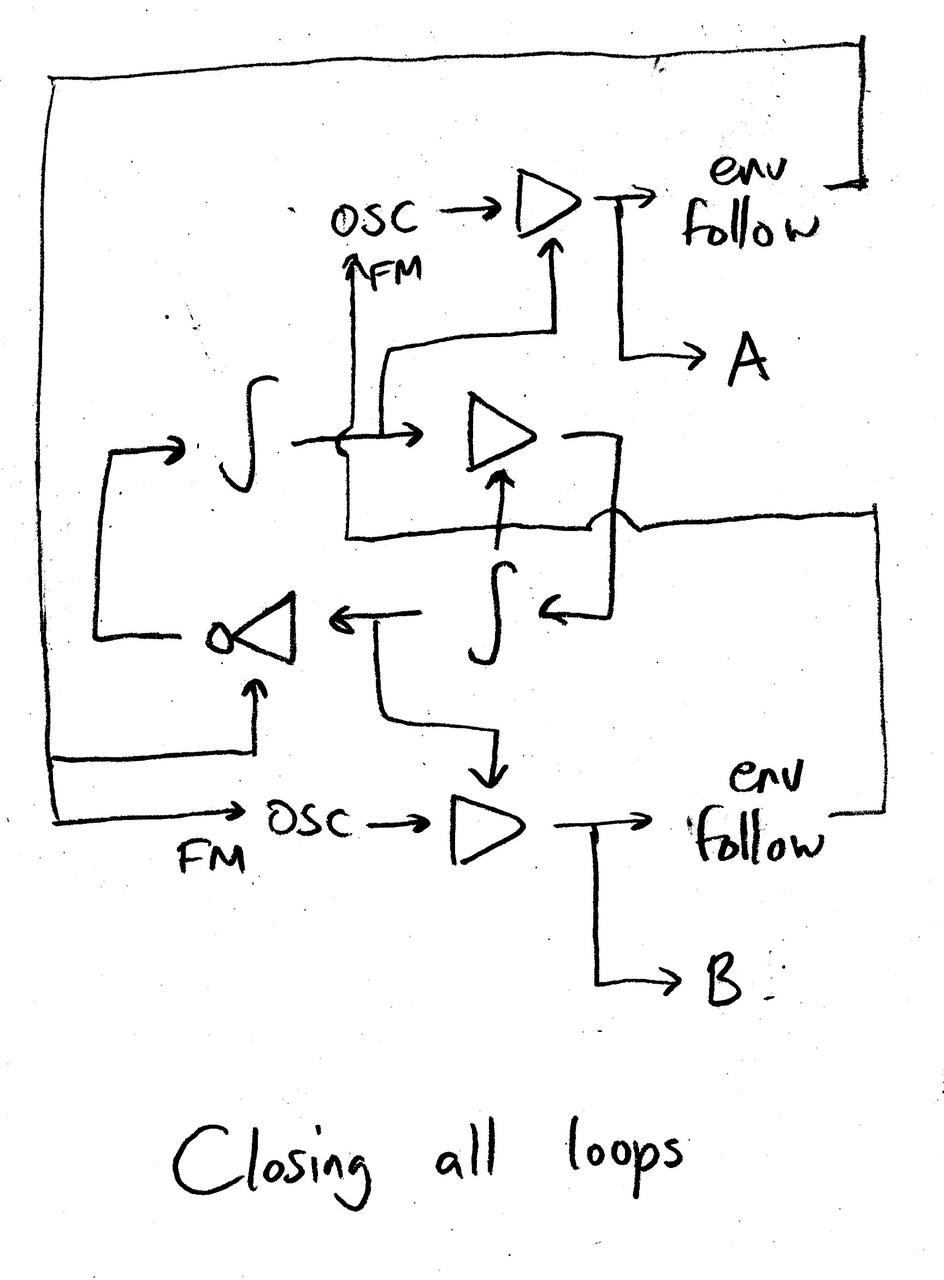
(I’m misusing notation here a bit; the arrows into the loop VCAs are not actually setting the gain, but wiggling around the gain it had in the previous diagram. The intentions of this diagram are more romantic than schematic — the point is to illustrate the closing of loops, not to specify an exact algorithm.)
This isn’t an actual simple harmonic oscillator anymore, but it mimics the core behavior of one. However, if we start changing any parameter, the core behavior of the “LFO” starts changing too. Everything interacts with everything, and nothing is isolated or purely upstream or purely downstream.
We’ll return to this patch and expand it into something more compelling in sound design terms. Let’s go theoretical for a bit and explain what we’re actually trying to do here.
Rules for Cybernetic Synthesis
Building off La Synthèse Humaine, Lines, and my own experiments, I suggest the following rules as my own interpretation of cybernetic synthesis. I’m not proffering a serious hypothesis on how Kayn and Vink worked — that’s more fun as secrets — instead, I’m trying to impose cybernetic-inspired constraints on myself to see if any interesting musical ideas emerge, especially ones that resemble their music. In this vein, I offer the following rules.
These don’t have precise mathematical meanings, and they’re about attitude and philosophy over signal processing. Even then, they’re restrictive: the vast majority of electronic music production workflows, including my typical process, are clearly not cybernetic. Top-down sequencing of musical events, whether manually entered or generated by algorithms, is entirely disallowed in this paradigm. Most of us employ a separation of concerns between sequencing and synthesizer; in cybernetic synthesis, my experience is that these systems necessarily have to be blurred, with the synthesis and sequencing “melting” into each other. We saw in the above example that we didn’t make explicit note events to speak of, but rather they emerged from the system.
It’s important to note here that the mere presence of feedback isn’t sufficient for a system to be cybernetic. Cybernetic synthesis is more radical than that: it demands that everything ultimately affects everything else in feedback. It could be one big loop, it could be multiple interacting loops, but there cannot be any signal flow that’s completely unidirectional. In graph theory terms, we could say that the directed graph of signal flow should be strongly connected, meaning there is a directed path from every node to every other node.
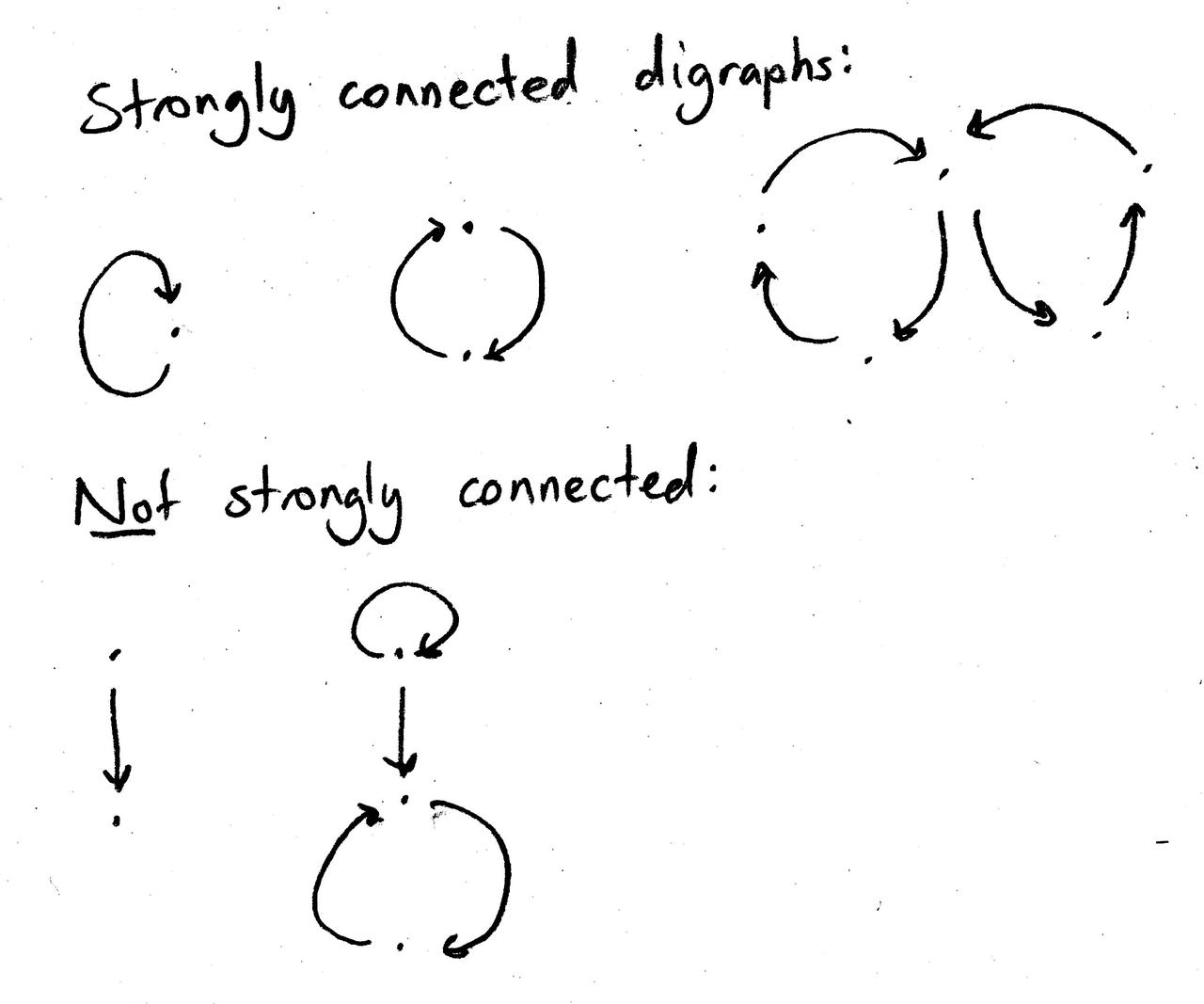
This feedback has to actually matter as well — you can multiply an otherwise open-loop signal by -100 dB and feed it back into the system, and you could technically lawyer your way into saying it’s closed-loop, but it won’t change much and therefore doesn’t really qualify as a cycle. (Switching, amplifying, or multiplexing can disable a loop temporarily, I consider this okay as long as it gets enabled and impacts everything else at some point.) Turning almost any knob should have a pretty major impact on the whole patch, an impact that is hopefully unpredictable.
Extending the cybernetic oscillator
That’s all nice, but I’m itching to get some legitimate sounds here. Let’s start by extend the signal path. Kayn uses a lot of reverb, so an obvious choice would be to throw some ‘verb on those oscillators, and reduce the highs. I’ve also changed the oscillator frequencies. Both the reverbs and the filters are in the feedback loop, so they also impact the operation of the core simple harmonic oscillator.
I would like some contrast with static and dynamic pitches for the oscillators. So let’s conditionally shut off the frequency modulation. A cybernetic way to do this would be to take the integral of some envelope follower, and switch off the modulation if the integral exceeds a threshold. To turn it back on again, the integral can wrap around back to 0 if it exceeds another threshold.
I also changed a bunch of other parameters here, but the little “whines” that start happening later were not something I anticipated.
The undulation that the core SHO created is very hard to make out now. That’s totally fine — cybernetic patches can go in completely different directions from what you intended. It calls into question whether it was worth starting with an SHO in the first place, but hindsight 20/20.
After an additional hour or two of throwing things at the wall, adding various areas of feedback and EQ and filtering and switches controlled by integrated envelope followers, and I got this:
This is completely autonomous, there is no live interaction in this recording. (It is also deterministic, there are no noise sources.) Don’t know about you, but I think it sounds reasonably Kaynian. True Kayn fans are free to roast me on the inaccuracy, but more importantly it’s a sound I like and would not have gotten otherwise, which is all I need for a successful experiment.
Part of the whole cybernetics deal, at least as I understand it, is that the human musician is also an integral part of the system — involved in its construction and usage in a bidirectional feedback loop. It’s for this reason that I don’t plan on sharing the SuperCollider source code here. To really learn how this process works, you have to just dig in and build your own patch from scratch. Having now spent a small amount of time on the builder’s side of things, the relative mystery around Kayn and Vink’s technical methods starts to make more sense to me. It’s hard to explain a system that grows organically and that I don’t fully understand myself!
Discussion
Previous work of mine on intentionally unpredictable audio systems include Feedback Integrator Networks and Matrix Modular Synthesis.
My typical process as a sound designer is as “top down” as it can be. I conceptualize a sound (or listen to a reference) and realize it as a patch, and while spontaneous and exploratory moments happen when working with synthesizers, full-on surprises have happened less and less often as I develop specific habits and go-to sound design patches. The “top down” nature goes out the window in cybernetic synthesis — with these rules, I’ve specifically denied myself the ability to know exactly what’s going to emerge. For a cybernetic synthesizer patch to do anything interesting, it has to be unpredictable at a fundamental level. It’s about receding control to emergent behavior, and this is what makes cybernetic sound design both rewarding and frustrating.
The very mention of chaos theory will certainly make a subset of my reader base perk up. I didn’t touch on chaos here because I didn’t want to imply that cybernetic systems have to exhibit chaos, but it’s certainly true that chaos is cybernetics’ rockstar nephew, and it’s perfectly applicable here. (The system that I built for this might already be chaotic, but I’m reluctant to use the term without checking things like the Lyapunov exponent.) If you’re really set on chaos, the core network of the simple harmonic oscillator can be replaced with a Duffing oscillator or a Lorenz attractor, but remember that these systems are only chaotic with certain parameter settings and some can be easily knocked into periodic or static behavior. It’s chaos, the entire point is that it’s difficult to predict.