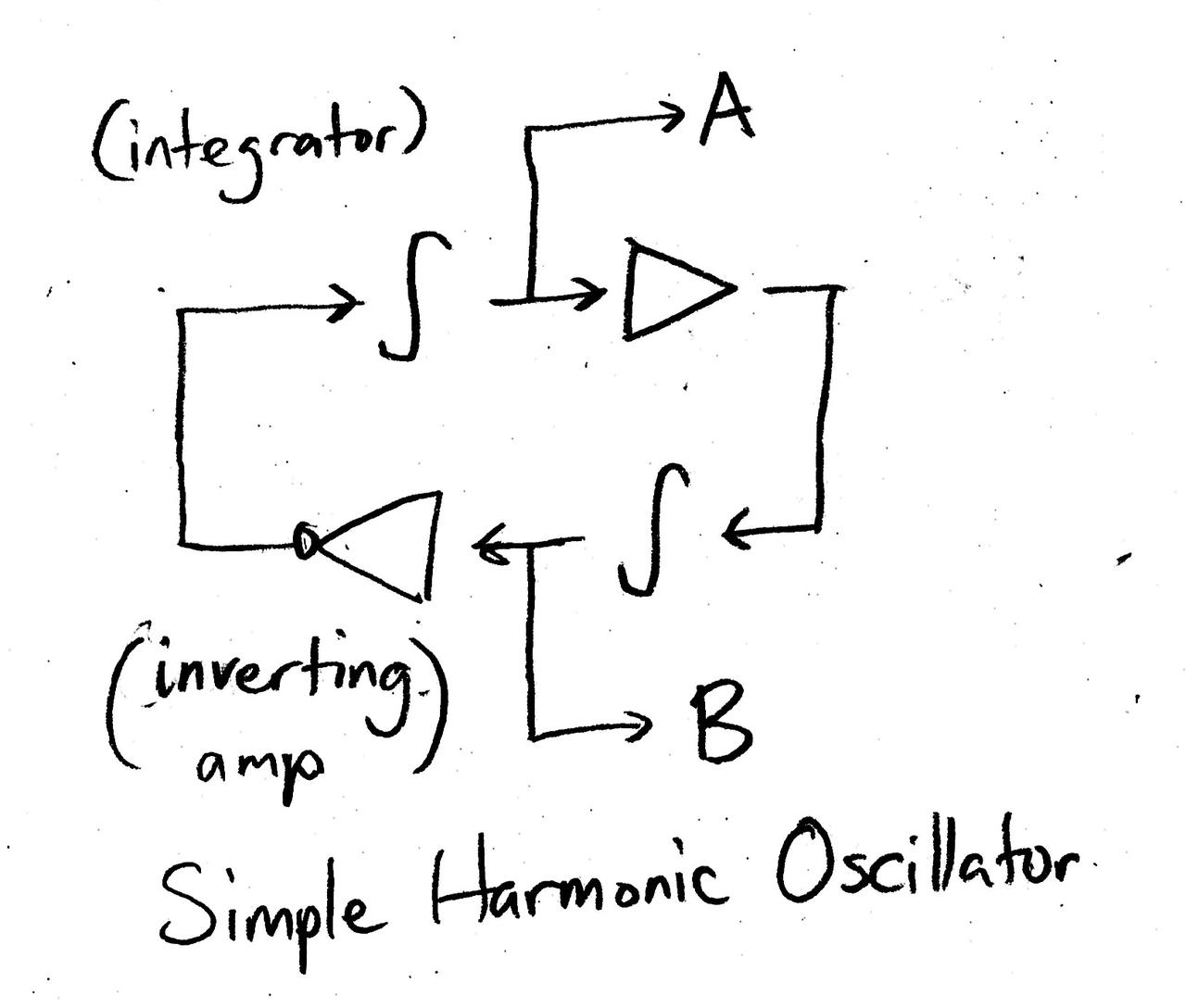
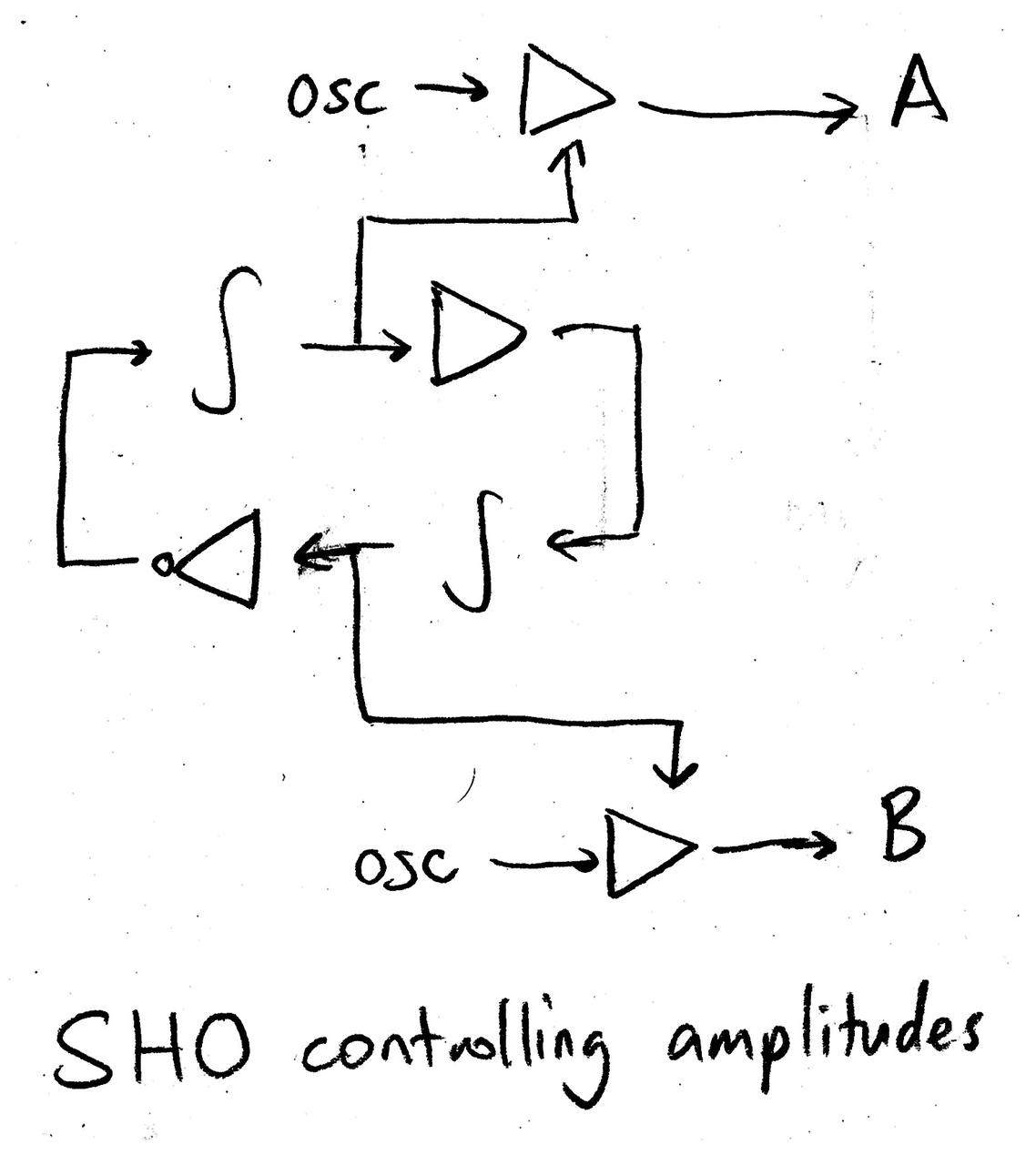
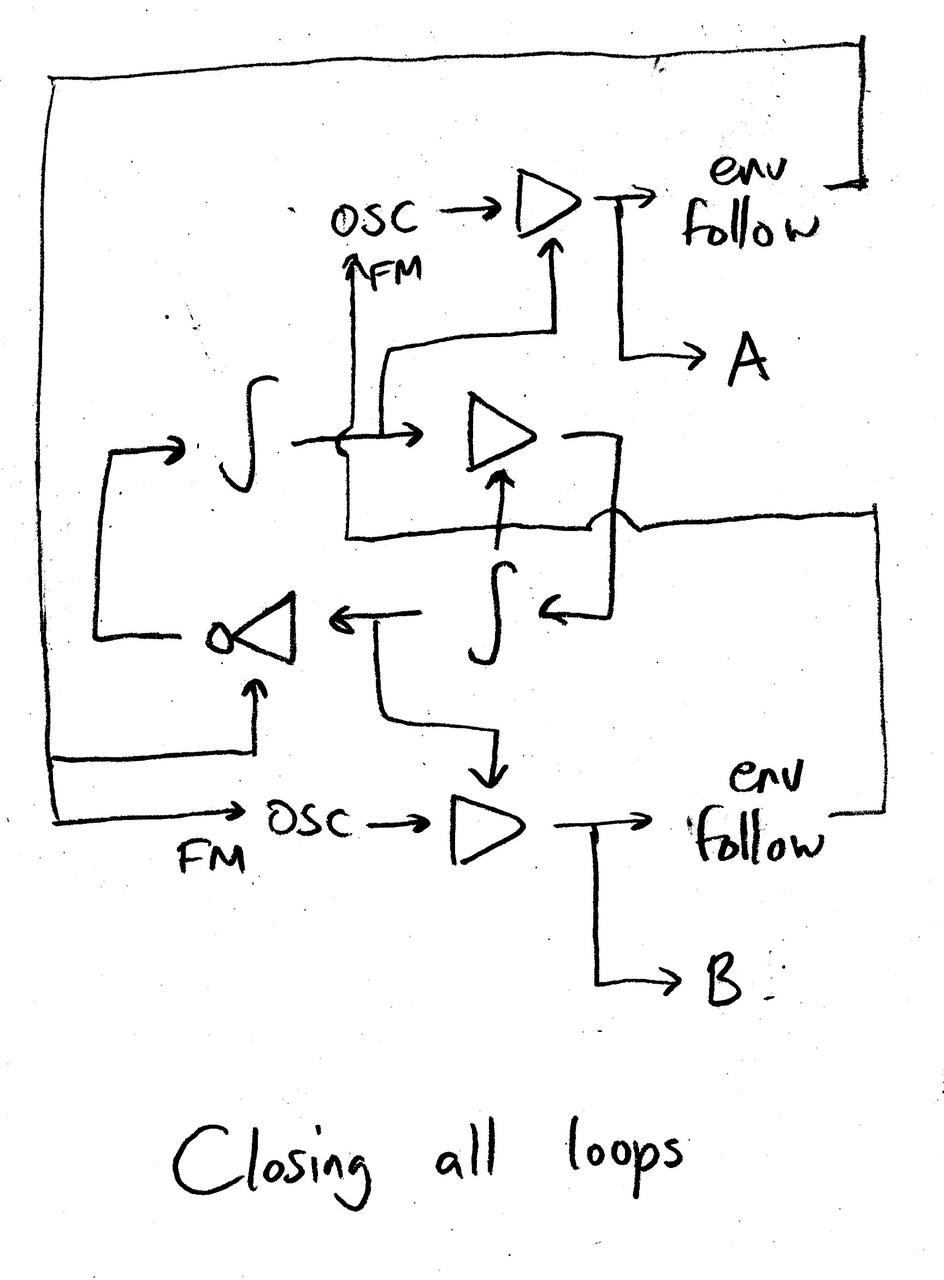
DM Synthesis
A while back, I tried recreating the sound of a dialup modem from scratch, which involved a dive into multiple PDFs of telecommunication standards. (I am not the first person to do this.) Very helpful was Windy Tan’s beautiful analysis breaking down a spectrogram of a real dialup handshake. A particularly famous bit is the nasal mid-low “whine” at the end of the handshake, and if you’ve ever wondered what that is, you’re hearing line probing signals L1 and L2, which are synthesized using additive synthesis. The exact partial frequency, phases, and amplitudes are specified in section 10.1.2.4 of ITU-T V.34. They’re at 9 seconds in this recording of a modem by thearchiveguy99 on Freesound:
WARNING: Audio files in this post are loud and piercing. Please turn up your speakers to extremely painful levels for optimal telecommunication.
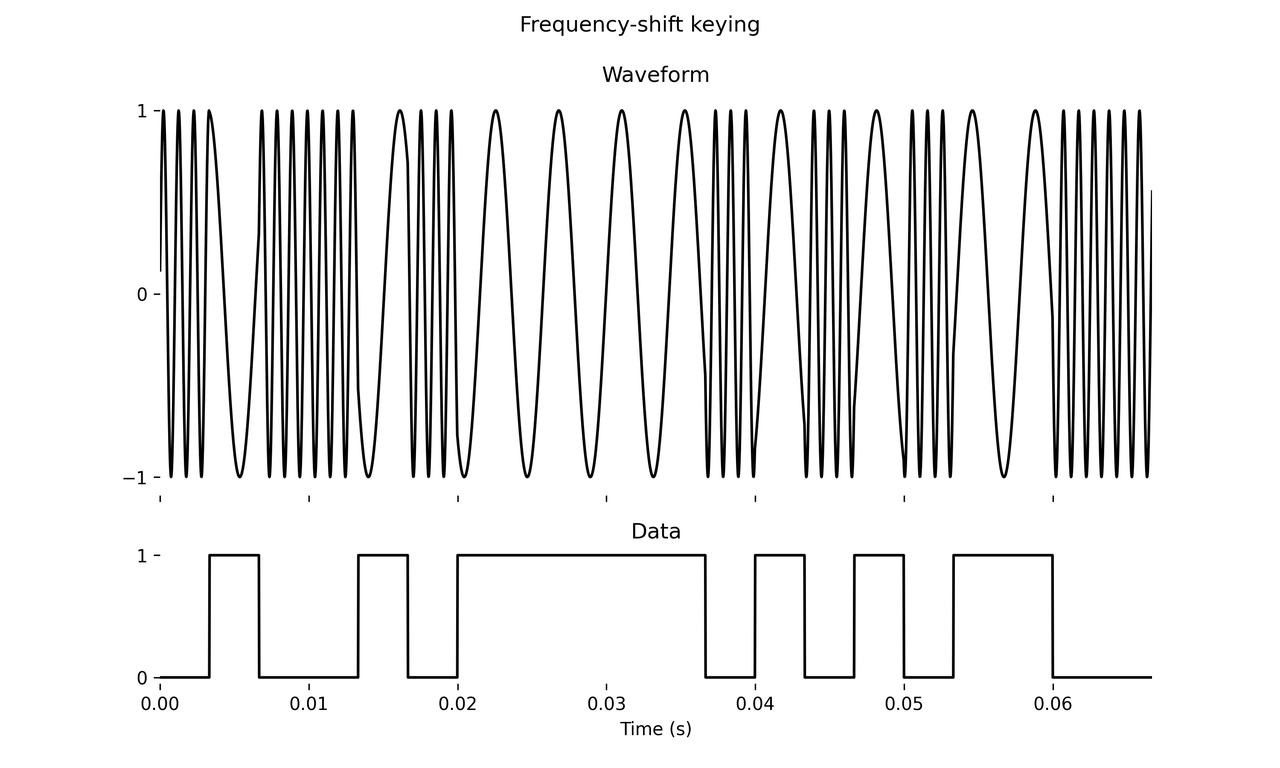
The whine is legendary, but I want to turn your attention to high-frequency gurgles before it, starting at about 4 seconds in, some of them resembling slurping a last bit of soda through a straw in a McDonald’s cup. These tones, specified at a high level in ITU-T V.8bis, are encoded using frequency-shift keying (FSK) as given in the lower-level ITU-T V.21 spec. In its simplest form, FSK uses a single sine wave to encode a binary signal by modulating its frequency. Following V.21’s description of a “channel 1” signal, at regular intervals of 1/300 seconds, a single bit is transmitted. If the bit is 0, the sine wave’s frequency is set to 1180 Hz. If the bit is 1, the frequency is set to 980 Hz.
Yep, that’s a dialup gurgle. The graph below demonstrates this visually (for different parameters — I had to lower the carrier for the 1 bits so that the distinction between the two is obvious). Above we have the audio waveform, below it the data signal.
Designing that dialup imitation made me realize that I really like how FSK sounds purely as a sound design tool. This got me looking into its various siblings, which are known as the “digital modulation” schemes for transmission of digital signals over an analog medium such as radio. In contrast, in “analog modulation” the signal being transmitted is continuous, encompassing familiar techniques like FM, AM, and single-sideband modulation. Today we’re going to honor the long tradition of adapting telecommunications methods for creative use by seeing what kind of sounds we can design by directly listening to signals produced with FSK and related methods. I call this approach Digital Modulation Synthesis, a name I’m not in love with, but I couldn’t think of a better one. It may be abbreviated to the cooler-sounding “DM Synthesis.”
In telecommunications, modulation is only half the story, and you also need a demodulator which takes the transmission signal and gets the data back. Engineering modulators and demodulators in a way that’s robust to noise is an interesting problem subject to nearly a century of study, but here we’re going to be the weirdos who just want to listen to the modulated signal itself. I will spend no time here discussing the engineering tradeoffs of these digital modulation schemes in a telecommunication settings; those problems are very interesting and deep but not relevant to this post.
This post is pretty light on math, and the DSP isn’t fancy here, as our concentration is more on sound design and synthesis. All this should be doable in SuperCollider, Pd, Max, etc. with pre-existing units.
I didn’t research this post as thoroughly as I would have liked, so it’s not impossible that I have misrepresented things from the telecommunications literature. If there are mistakes, sorry about that.